题目内容
【题目】正四面体ABCD的棱长为2,棱AD与平面α所成的角θ∈[ ![]() ,
, ![]() ],且顶点A在平面α内,B,C,D均在平面α外,则棱BC的中点E到平面α的距离的取值范围是( )
],且顶点A在平面α内,B,C,D均在平面α外,则棱BC的中点E到平面α的距离的取值范围是( ) 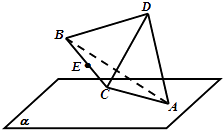
A.[ ![]() ,1]
,1]
B.[ ![]() ,1]
,1]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
【答案】C
【解析】解:取平面DEA⊥平面α位置考虑即可.如图所示,
在△ADE中,AD=2,DE=AE= ![]() ,
,
∴cos∠DAE= ![]() =
= ![]() ,
,
棱AD与平面α所成的角为 ![]() 时,sin∠EAN=sin(
时,sin∠EAN=sin( ![]() ﹣∠DAE)
﹣∠DAE)
= ![]() =
= ![]() ,
,
∴EN= ![]() (
( ![]() )=
)= ![]()
或sin∠EAN=sin( ![]() +∠DAE)=
+∠DAE)= ![]()
∴EN= ![]() (
( ![]() )=
)= ![]()
∴棱BC的中点E到平面α的距离的取值范围是[ ![]() ,
, ![]() ].
].
故选:C.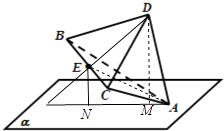

练习册系列答案
相关题目



