题目内容
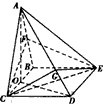
四棱锥A-BCDE中,底面BCDE为矩形,侧面ABC⊥底面BCDE,BC=2,CD= ,AB=AC。
,AB=AC。
 ,AB=AC。
,AB=AC。
(1)证明:AD⊥CE;
(2)设CE与平面ABE所成的角为45°,求二面角C-AD-E的大小。
(2)设CE与平面ABE所成的角为45°,求二面角C-AD-E的大小。
| 解:(1)证明:作AO⊥BC,垂足为O,连结OD 由题设知,AO⊥底面BCDE,且O为BC中点 由 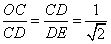 知Rt△OCD∽Rt△CDE 从而∠ODC=∠CED, 于是CE⊥OD 由三垂线定理知,AD⊥CE; (2)由题意,BE⊥BC,所以BE⊥平面ABC, 又BE 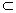 平面ABE, 平面ABE,所以平面ABE⊥平面ABC 作CF⊥AB,垂足为F,连结FE,则CF⊥平面ABE 故∠CEF为CE与平面ABE所成的角,∠CEF =45° 由CE= 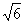 ,得CF= ,得CF=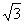 又BC=2,因而∠ABC=60° 所以△ABC为等边三角形 作CG⊥AD,垂足为G,连结GE 由(1)知,CE⊥AD,又CE∩CG=C 故AD⊥平面CGE,AD⊥GE, ∠CGE是二面角C-AD-E的平面角 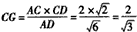 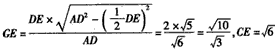 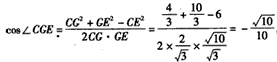 所以二面角C-AD-E为 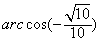 。 。 |
 |

练习册系列答案
相关题目
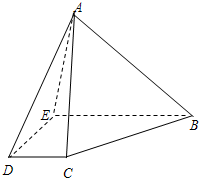 如图,在四棱锥A-BCDE中,底面BCDE是直角梯形,∠BED=90°,BE∥CD,AB=6,BC=5,
如图,在四棱锥A-BCDE中,底面BCDE是直角梯形,∠BED=90°,BE∥CD,AB=6,BC=5,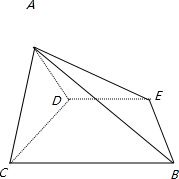
 如图,四棱锥A-BCDE中,△ABC是正三角形,四边形BCDE是矩形,且平面ABC⊥平面BCDE,AB=2,AD=4.
如图,四棱锥A-BCDE中,△ABC是正三角形,四边形BCDE是矩形,且平面ABC⊥平面BCDE,AB=2,AD=4. 如图,四棱锥A-BCDE中,△ABC是正三角形,四边形BCDE是矩形,且平面ABC⊥平面BCDE,AB=2,AD=4.
如图,四棱锥A-BCDE中,△ABC是正三角形,四边形BCDE是矩形,且平面ABC⊥平面BCDE,AB=2,AD=4. 如图,四棱锥A-BCDE中,侧面△ADE是等边三角形,在底面等腰梯形BCDE中,CD∥BE,DE=2,CD=4,∠CDE=60°,M为DE的中点,F为AC的中点,AC=4.
如图,四棱锥A-BCDE中,侧面△ADE是等边三角形,在底面等腰梯形BCDE中,CD∥BE,DE=2,CD=4,∠CDE=60°,M为DE的中点,F为AC的中点,AC=4.