题目内容
在(| 2 |
| 3 | 3 |
分析:利用二项展开式的通项公式求出通项,令各项的指数为整数,求出系数为有理数的项.
解答:解:(
x+
y)100的展开式的通项Tr+1=C100r•((
x)100-r•(
y)r=C100r•2
•3
,
该项的系数为C100r•2
•3
,,
要满足C100r•2
•3
,是有理数,则r应是6的倍数.
∵0≤r≤100且r∈Z,∴r=0,6,12,18,,96
∴系数为有理数的项共有17项.
故答案为17
| 2 |
| 3 | 3 |
| 2 |
| 3 | 3 |
| 100-r |
| 2 |
| r |
| 3 |
该项的系数为C100r•2
| 100-r |
| 2 |
| r |
| 3 |
要满足C100r•2
| 100-r |
| 2 |
| r |
| 3 |
∵0≤r≤100且r∈Z,∴r=0,6,12,18,,96
∴系数为有理数的项共有17项.
故答案为17
点评:本题考查利用二项展开式的通项公式解决二项展开式的特定项问题.

练习册系列答案
相关题目
 18、某次考试中,某班级的数学成绩统计图如下.下列说法错误的是
18、某次考试中,某班级的数学成绩统计图如下.下列说法错误的是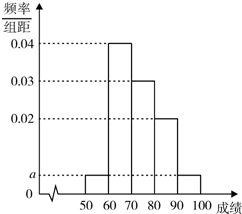 某校高二年级100名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100),则这100名学生数学成绩在[70,100]分数段内的人数为( )
某校高二年级100名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100),则这100名学生数学成绩在[70,100]分数段内的人数为( )