题目内容
已知点(a,b)中a,b分别表示男生小A,女生小W随机的到教室的时间,其中a,b∈[7,9],则a,b使方程x2-2(a-8)x+(b-8)2=0有实根的概率为( )A.

B.

C.
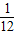
D.
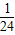
【答案】分析:由a从区间[7,9]中任取一个数,b从区间[7,9]中任取一个数得试验的全部结果构成区域Ω={(a,b)|7≤a≤9,7≤b≤9},而方程f(x)=0有实根构成的区域为M={(a,b)|7≤a≤9,7≤b≤9,|a-8|≥|b-8|},分别求出两个区域面积即可得到概率.
解答: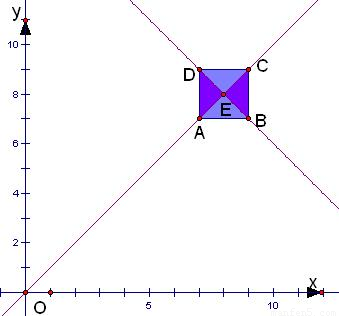 解:∵a从区间[7,9]中任取一个数,b从区间[7,9]中任取一个数
解:∵a从区间[7,9]中任取一个数,b从区间[7,9]中任取一个数
则试验的全部结果构成区域Ω={(a,b)|7≤a≤9,7≤b≤9}这是一个正方形区域,其面积SΩ=2×2=4
设“方程x2-2(a-8)x+(b-8)2=0有实根”为事件B
则事件B构成的区域为M={(a,b)|7≤a≤9,7≤b≤9,△≥0}={(a,b)|7≤a≤9,7≤b≤9,|a-8|≥|b-8|}即图中阴影部分的两个三角形ADE和三角形BCE,其面积SM= ×2×2=2
×2×2=2
由几何概型的概率计算公式可得方程f(x)=0没有实根的概率P(B)=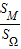 =
= .
.
故选A.
点评:本题主要考查一元二次方程的根的分布与系数的关系,以及几何概型的概率计算,属于中档题.
解答:
 解:∵a从区间[7,9]中任取一个数,b从区间[7,9]中任取一个数
解:∵a从区间[7,9]中任取一个数,b从区间[7,9]中任取一个数则试验的全部结果构成区域Ω={(a,b)|7≤a≤9,7≤b≤9}这是一个正方形区域,其面积SΩ=2×2=4
设“方程x2-2(a-8)x+(b-8)2=0有实根”为事件B
则事件B构成的区域为M={(a,b)|7≤a≤9,7≤b≤9,△≥0}={(a,b)|7≤a≤9,7≤b≤9,|a-8|≥|b-8|}即图中阴影部分的两个三角形ADE和三角形BCE,其面积SM=
 ×2×2=2
×2×2=2由几何概型的概率计算公式可得方程f(x)=0没有实根的概率P(B)=
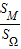 =
= .
.故选A.
点评:本题主要考查一元二次方程的根的分布与系数的关系,以及几何概型的概率计算,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
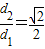 .
.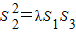 成立.若存在,求出λ的值;若不存在,请说明理由.
成立.若存在,求出λ的值;若不存在,请说明理由.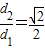 .
.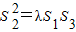 成立.若存在,求出λ的值;若不存在,请说明理由.
成立.若存在,求出λ的值;若不存在,请说明理由.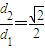 .
.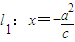 、点F(-c,0)、曲线C:
、点F(-c,0)、曲线C: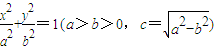 ,则使等式S22=λS1S3成立的λ的值仍保持不变.请给出你的判断______ (填写“不正确”或“正确”)(限于时间,这里不需要举反例,或证明).
,则使等式S22=λS1S3成立的λ的值仍保持不变.请给出你的判断______ (填写“不正确”或“正确”)(限于时间,这里不需要举反例,或证明).