题目内容
已知函数![]() 是函数
是函数![]() 的导函数,设
的导函数,设![]()
(I)证明:数列![]() 是等比数列,并求出数列
是等比数列,并求出数列![]() 的通项公式;
的通项公式;
(II)令![]() 的前n项和
的前n项和![]()

(Ⅱ)由题意![]()
则![]() -----------------------------7
-----------------------------7![]() 分
分
![]() ------------------------------------------------------9分
------------------------------------------------------9分
令![]() ①
①
①×![]() 得:
得:![]() ②
②
①![]() ②得:
②得:
即![]() ------------------------------------12分
------------------------------------12分
所以![]() ---------------------------
---------------------------![]() ---13分
---13分

练习册系列答案
相关题目
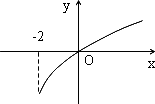
已知函数f(x)的定义域为[-3,+∞),部分函数值如表所示,其导函数的图象如图所示,若正数a,b满足f(2a+b)<1,则
的取值范围是( )

| b+2 |
| a+2 |

A、(
| ||
B、(
| ||
| C、(1,4) | ||
D、(-∞,
|
 已知函数f(x)的定义域为[-2,+∞),部分函数值如下表,f'(x)为f(x)的导函数,f'(x)的图象如图所示.如果实数a满足f(a)<1,则a的取值范围是( ) 已知函数f(x)的定义域为[-2,+∞),部分函数值如下表,f'(x)为f(x)的导函数,f'(x)的图象如图所示.如果实数a满足f(a)<1,则a的取值范围是( )
|
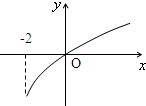 已知函数f(x)的定义域为[-2,+∞),部分函数值如下表,f'(x)为f(x)的导函数,f'(x)的图象如图所示.如果实数a满足f(a)<1,则a的取值范围是
已知函数f(x)的定义域为[-2,+∞),部分函数值如下表,f'(x)为f(x)的导函数,f'(x)的图象如图所示.如果实数a满足f(a)<1,则a的取值范围是
| x | -2 | 0 | 4 |
| f(x) | 1 | -1 | 1 |
- A.(-2,0)
- B.(0,4)
- C.(-2,4)
- D.[-2,4)
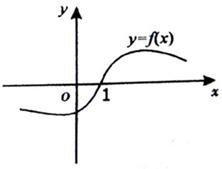 已知函数f(x)(x∈R)的一段图象如图所示,f′(x)是函f(x)(数的导函数,且y=f(x+1)是奇函数,给出以下结论:
已知函数f(x)(x∈R)的一段图象如图所示,f′(x)是函f(x)(数的导函数,且y=f(x+1)是奇函数,给出以下结论: