题目内容
已知三棱锥A―BCD的侧棱AB⊥底面BCD,BC = CD,∠BCD = 90°,∠ADB = 30°,E、F分别是侧棱AC、AD的中点.
(1)求证:平面BEF⊥平面ABC;
(2)求平面BEF和平面BCD所成的角.
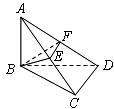
解:(1)∵AB⊥底面BCD,∴AB⊥CD,又∵BC⊥CD,∴CD⊥平面ABC.
∵E、F分别为AC、AD的中点,∴EF∥CD.
∴EF⊥平面ABC,∴平面BEF⊥平面ABC.
(2)设平面BEF与面BCD交线为l,则B∈l (如图).
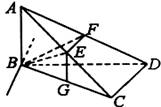
∵EF∥DC,![]() 面BEF,∴DC∥面BEF.
面BEF,∴DC∥面BEF.
∵面BCD∩面BEF = l,![]() 面BCD,∴DC∥l.
面BCD,∴DC∥l.
又DC⊥平面ABC,∴l⊥面ABC. 面ABC与面BEF、面BCD交于BE、BC,
∴∠EBC是二面角BEF―l―BDC所成的平面角.
过E作EG⊥BC于G,又AB⊥BC,
∴EG∥AB,且EG =![]() AB.
AB.
设BC = CD = 1,则BG =![]() ,BD =
,BD =![]() ,
,
又∠ADB = 30°,∴![]() .
.
∴tan∠EBG =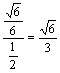 . ∴平面BEF和平面BCD所成的角为arctan
. ∴平面BEF和平面BCD所成的角为arctan![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
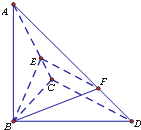 已知三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是直线AC,AD上的点,且
已知三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是直线AC,AD上的点,且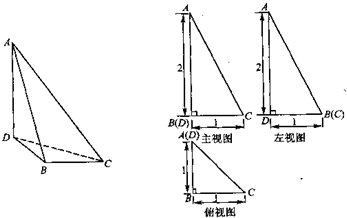 (2009•大连一模)已知三棱锥A-BCD及其三视图如图所示.
(2009•大连一模)已知三棱锥A-BCD及其三视图如图所示.