Question

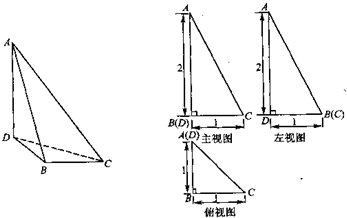（2009•大连一模）已知三棱锥A-BCD及其三视图如图所示．
（I）若DE⊥AB于E，DE⊥AC于F，求证：AC⊥平面DEF；
（Ⅱ）求二面角B-AC-D的大小．

Answer 1

分析：（Ⅰ）由三视图可知三棱锥A-BCD的底面是等腰直角三角形，且直角边长为1，每个侧面都是直角三角形，且棱锥的高AD=2，利用线面垂直的判定和性质可以证得AC⊥DE，又DF⊥AC，则可得到线面垂直；
（Ⅱ）由（Ⅰ）可知∠DFE为二面角B-AC-D的平面角，分别在直角三角形ADB和直角三角形ADC中求出斜边上的高DE、DF，则二面角B-AC-D的大小可求．

解答：（I）证明：由三视图可得，三棱锥A-BCD中
∠ADB，∠ADC，∠DBC，∠ABC都等于90°，
每个面都是直角三角形；
如图，

可得CB⊥面ADB，所以CB⊥DE，
又DE⊥AB，AB∩BC=B，所以DE⊥面ABC，
而AC?面ABC，所以DE⊥AC，
又DF⊥AC，DE∩DF=D，所以AC⊥面DEF．
（II）解：由（I）知∠DFE为二面角B-AC-D的平面角，
在直角三角形ADB中，由AD=2，DB=1，所以AB=

5

，
所以DE=

AD•DB

AB

=

2×1

5

=

2 5

5

在直角三角形DBC中，因为DB=BC=1，所以DC=

2

，在直角三角形ADC中，
AD=2，DC=

2

，所以AC=

6

，
所以DF=

AD•DC

AC

=

2× 2

6

=

2 3

3

在直角三角形DEF中，
∴sin∠DFE=

DE

DF

=

2 5 5

2 3 3

=

15

5

．
∴∠DFE=arcsin

15

5

．

点评：本题考查直线与平面垂直的判定，考查了二面角的求法，考查了三视图，解答此题的关键是能根据三视图中的数据得到原几何体中量的关系，是中档题．