题目内容
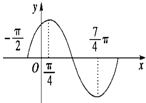 函数f(x)=3sin(ωx+?)
函数f(x)=3sin(ωx+?)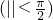 的图象如图所示.
的图象如图所示.
试依图推出:
(1)f(x)的解析式;
(2)f(x)的单调递增区间;
(3)f(x)的对称轴、对称中心.
解:(1)由图象可知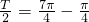 =
= ,
,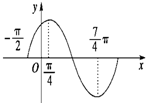
T=3π,ω= =
= ,因为函数的图象经过(
,因为函数的图象经过(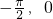 ),
),
所以0=3sin[ ×(-
×(- )+φ]=sin(
)+φ]=sin(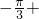 φ),
φ),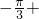 φ=kπ,k∈Z,
φ=kπ,k∈Z,
∵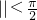 ,∴k=0时,φ=
,∴k=0时,φ= ,
,
所以所求函数的解析式为:(x)=3sin( x+
x+ ).
).
(2)由(1)以及函数的图象可知当x=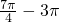 =-
=- 时,函数f(x)取得最小值,
时,函数f(x)取得最小值,
∴f(x)的单调增区间是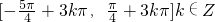 .
.
(3)由图象以及函数的表达式可知 x+
x+ =kπ+
=kπ+ ,k∈Z,
,k∈Z,
解得x=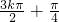 ,k∈Z,此为函数的对称轴方程.
,k∈Z,此为函数的对称轴方程.
 x+
x+ =kπ,k∈Z,此时x=
=kπ,k∈Z,此时x=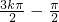 ,f(x)=0,
,f(x)=0,
所以函数的对称中心为(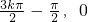 ).
).
分析:(1)利用函数的图象求出函数的周期,然后求出ω,利用函数通过(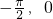 ),求出φ,即可求解f(x)的解析式;
),求出φ,即可求解f(x)的解析式;
(2)借助函数的图象求出函数最小值时距离原点最近的x值,即可求解f(x)的单调递增区间;
(3)利用函数的最值求出f(x)的对称轴方程,利用正弦函数的对称中心,求解函数的对称中心.
点评:本题考查函数的解析式的求法,函数的单调增区间的求法,对称中心与对称轴方程的求法,考查计算能力.
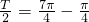 =
= ,
,
T=3π,ω=
 =
= ,因为函数的图象经过(
,因为函数的图象经过(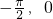 ),
),所以0=3sin[
 ×(-
×(- )+φ]=sin(
)+φ]=sin(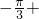 φ),
φ),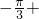 φ=kπ,k∈Z,
φ=kπ,k∈Z,∵
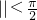 ,∴k=0时,φ=
,∴k=0时,φ= ,
,所以所求函数的解析式为:(x)=3sin(
 x+
x+ ).
).(2)由(1)以及函数的图象可知当x=
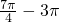 =-
=- 时,函数f(x)取得最小值,
时,函数f(x)取得最小值,∴f(x)的单调增区间是
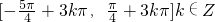 .
.(3)由图象以及函数的表达式可知
 x+
x+ =kπ+
=kπ+ ,k∈Z,
,k∈Z,解得x=
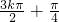 ,k∈Z,此为函数的对称轴方程.
,k∈Z,此为函数的对称轴方程. x+
x+ =kπ,k∈Z,此时x=
=kπ,k∈Z,此时x=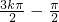 ,f(x)=0,
,f(x)=0,所以函数的对称中心为(
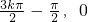 ).
).分析:(1)利用函数的图象求出函数的周期,然后求出ω,利用函数通过(
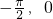 ),求出φ,即可求解f(x)的解析式;
),求出φ,即可求解f(x)的解析式;(2)借助函数的图象求出函数最小值时距离原点最近的x值,即可求解f(x)的单调递增区间;
(3)利用函数的最值求出f(x)的对称轴方程,利用正弦函数的对称中心,求解函数的对称中心.
点评:本题考查函数的解析式的求法,函数的单调增区间的求法,对称中心与对称轴方程的求法,考查计算能力.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目