题目内容
已知非零向量
,
满足
+3
与7
-5
互相垂直,
-4
与7
-2
互相垂直,则
与
的夹角为
.
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| π |
| 3 |
| π |
| 3 |
分析:由题意可得
,联立可解得
2=2
•
,|
|=|
|,代入向量的夹角公式可得其余弦值,由夹角的范围可得.
|
| b |
| a |
| b |
| a |
| b |
解答:解:设
与
的夹角为θ,θ∈[0,π]
由题意可得
,
即
,
②-①可得23
2-46
•
=0,即
2=2
•
,
再代入①可得
2=
2,即|
|=|
|,
∴cosθ=
=
,又θ∈[0,π]
∴θ=
故答案为:
| a |
| b |
由题意可得
|
即
|
②-①可得23
| b |
| a |
| b |
| b |
| a |
| b |
再代入①可得
| a |
| b |
| a |
| b |
∴cosθ=
| ||||
|
|
| 1 |
| 2 |
∴θ=
| π |
| 3 |
故答案为:
| π |
| 3 |
点评:本题考查向量的夹角与向量的数量积的关系,属中档题.

练习册系列答案
相关题目
已知非零向量
与
满足(
+
)•
=0,且
•
=-
,则△ABC为( )
| AB |
| AC |
| ||
|
|
| ||
|
|
| BC |
| ||
|
|
| ||
|
|
| 1 |
| 2 |
| A、等腰非等边三角形 |
| B、等边三角形 |
| C、三边均不相等的三角形 |
| D、直角三角形 |
 、
、 、
、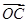 、
、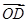 满足:
满足: ,=
,=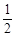 ,g,则A、B、C、D四点在同一平面上;
,g,则A、B、C、D四点在同一平面上; ,<
,< ,则|
,则|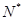 ,若a2,=a2009,g,且A、B、C三点共线,但O点不在直线BC上,则
,若a2,=a2009,g,且A、B、C三点共线,但O点不在直线BC上,则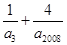 的最小值为10;
的最小值为10; ,=
,= ,g,则A、B、C三点共线且A分
,g,则A、B、C三点共线且A分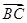 所成的比一定为4
所成的比一定为4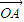 、
、 、
、 、
、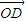 满足:
满足: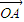 =α
=α Z+β
Z+β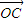 Z+γ
Z+γ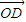 Z(α,β,γ∈R),B、C、D为不共线三点,给出下列命题:
Z(α,β,γ∈R),B、C、D为不共线三点,给出下列命题: ,β=
,β= ,γ=-1,则A、B、C、D四点在同一平面上;
,γ=-1,则A、B、C、D四点在同一平面上; Z|+|
Z|+| |+|
|+| |=1,<
|=1,< ,
, >=<
>=<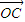 ,
, >=
>= ,<
,<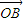 ,
,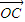 >=
>=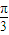 ,则|
,则| |=2;
|=2; 的最小值为10;
的最小值为10; ,β=-
,β=- Z,γ=0,则A、B、C三点共线且A分
Z,γ=0,则A、B、C三点共线且A分 所成的比λ一定为-4
所成的比λ一定为-4