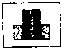题目内容
15、如图，立体图形A-BCD的四个面分别为△ABC、△ACD、△ADB和△BCD，E、F、G分别是线段AB、AC、AD上的点，且满足AE：AB=AF：AC=AG：AD，求证：△EFG∽△BCD．
分析：由两个三角形相似的判定定理，只要两对应边相似，夹角相等即可．由AE：AB=AF：AC=AG：AD，
易得EG∥BD，GF∥DC且比例相等．
易得EG∥BD，GF∥DC且比例相等．
解答：证明：在△ABD中，
∵AE：AB=AG：AD，
∴EG∥BD．同理，GF∥DC，EF∥BC．
又∠GEF与∠DBC方向相同．
∴∠GEF=∠DBC．
同理，∠EGF=∠BDC．
∴△EFG∽△BCD．
∵AE：AB=AG：AD，
∴EG∥BD．同理，GF∥DC，EF∥BC．
又∠GEF与∠DBC方向相同．
∴∠GEF=∠DBC．
同理，∠EGF=∠BDC．
∴△EFG∽△BCD．
点评：本题考查两个三角形相似的判定、两条直线平行的判断、注意平面中直线平行的判定在空间中的应用．
练习册系列答案
相关题目
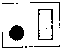
4、对于如图的立体图形，则它的侧视图是（ ）
的立方体内有1个大球和8个小球，大球与立方体的六个面都相切，每个小球与大球外切且与共顶点的三个面也相切，现在把立方体的每个角都截去一个三棱锥，截面都为正三角形并与小球相切，变成一个新的立体图形，则原立方体的每条棱还剩余
B．
C．
D．
对于如图的立体图形，则它的侧视图是
