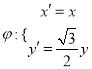题目内容
【题目】(本题满分12分)在平面直角坐标系xOy中,已知两点![]() 和
和![]() ,动点M满足
,动点M满足![]() ,设点M的轨迹为C,半抛物线
,设点M的轨迹为C,半抛物线![]() :
:![]() (
(![]() ),设点
),设点![]() .
.
(Ⅰ)求C的轨迹方程;
(Ⅱ)设点T是曲线![]() 上一点,曲线
上一点,曲线![]() 在点T处的切线与曲线C相交于点A和点B,求△ABD的面积的最大值及点T的坐标.
在点T处的切线与曲线C相交于点A和点B,求△ABD的面积的最大值及点T的坐标.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;
;![]() .
.
【解析】
试题分析:(Ⅰ)设点![]() ,则可得向量的坐标,根据向量数量积公式可求得点
,则可得向量的坐标,根据向量数量积公式可求得点![]() 的轨迹
的轨迹![]() 的轨迹方程.(Ⅱ)抛物线
的轨迹方程.(Ⅱ)抛物线![]() 为
为![]() ,设
,设![]() (
(![]() ),对
),对![]() 求导,根据导数的几何意义可得在点
求导,根据导数的几何意义可得在点![]() 处的切线的斜率,从而可得切线方程.将切线方程和曲线
处的切线的斜率,从而可得切线方程.将切线方程和曲线![]() 方程联立消去
方程联立消去![]() 整理为关于
整理为关于![]() 的一元二次方程.可知其判别式大于0,由韦达定理可得两根之和,两根之积.根据弦长公式可求得弦
的一元二次方程.可知其判别式大于0,由韦达定理可得两根之和,两根之积.根据弦长公式可求得弦![]() 由点到线的距离公式可求得三角形的高,从而可得三角形面积.配方法可求得其最值及取最值时
由点到线的距离公式可求得三角形的高,从而可得三角形面积.配方法可求得其最值及取最值时![]() 的值.
的值.
试题解析:解:(Ⅰ)设点![]() ,由
,由![]() ,得
,得![]() ,
,
所以![]() 的轨迹方程是
的轨迹方程是![]() ;(4分)
;(4分)
(Ⅱ)抛物线![]() 为
为![]() ,设
,设![]() (
(![]() ),则
),则![]() ,所以切线为:
,所以切线为:
![]() ,即
,即![]() ,联立
,联立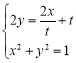 ,
,![]() ,
,
判别式△![]() ,设
,设![]() ,
,![]() ,则
,则![]() ,过点
,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,于是
,于是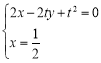 ,得
,得![]() ,则
,则![]() ,
,
故△ABD的面积![]()
![]()
![]() ,此时
,此时![]() .(12分)
.(12分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】一鲜花店根据一个月(30天)某种鲜花的日销售量与销售天数统计如下,将日销售量落入各组区间频率视为概率.
日销售量(枝) |
|
|
|
|
|
销售天数 | 3天 | 5天 | 13天 | 6天 | 3天 |
(1)试求这30天中日销售量低于100枝的概率;
(2)若此花店在日销售量低于100枝的时候选择2天作促销活动,求这2天恰好是在日销售量低于50枝时的概率.