题目内容
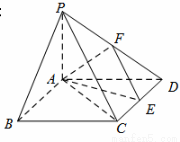
如图,在四棱锥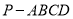 中,底面
中,底面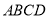 是矩形,
是矩形,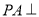 平面
平面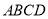 ,
,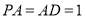 ,
, ,点
,点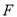 是
是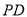 的中点,点
的中点,点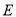 是边
是边 上的任意一点.
上的任意一点.
(Ⅰ)当点 为
为 边的中点时,判断
边的中点时,判断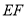 与平面
与平面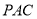 的位置关系,并加以证明;
的位置关系,并加以证明;
(Ⅱ)证明:无论点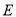 在
在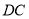 边的何处,都有
边的何处,都有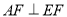 ;
;
(Ⅲ)求三棱锥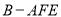 的体积.
的体积.
(Ⅰ)(Ⅱ)见解析;(Ⅲ)
【解析】
试题分析:(Ⅰ)当点 为
为 边的中点时,
边的中点时, 是
是 的中位线,故
的中位线,故 与平面
与平面 平行;(Ⅱ)要证明线线垂直,一般还是通过线面垂直来证明,本题中易证明
平行;(Ⅱ)要证明线线垂直,一般还是通过线面垂直来证明,本题中易证明 平面
平面 ,
, 平面
平面 ,所以
,所以 ,
, ,从而
,从而 平面
平面 ,
, ;(Ⅲ)作
;(Ⅲ)作 交
交 于
于 ,则
,则 平面
平面 ,且
,且 又
又



试题解析: (Ⅰ)当点 为
为 边的中点时,
边的中点时, 与平面
与平面 平行.
平行.
 在
在 中,
中, 、
、 分别为
分别为 、
、 的中点,
的中点,

 ,
,
又 平面
平面 ,而
,而 平面
平面 ,
,

 平面
平面 ; ..4分
; ..4分
(Ⅱ)证明:
 平面
平面 ,
, 平面
平面



 是矩形,
是矩形,


 ,
,
 平面
平面
又 平面
平面

 ...6分
...6分
又 ,点
,点 是
是 中点,
中点,
 ,
,
又


 平面
平面 ,
,

 平面
平面 ,
,
 .8分
.8分
(Ⅲ)作 交
交 于
于 ,则
,则 平面
平面 ,且
,且 .9分
.9分
又

 ,
,
 三棱锥
三棱锥 的体积为
的体积为 12分
12分
考点:线面位置关系、锥体体积

练习册系列答案
相关题目
 (x>0),观察:f1(x)=f(x)=
(x>0),观察:f1(x)=f(x)= , f3(x)=f(f2(x))=
, f3(x)=f(f2(x))= , f4(x)=f(f3(x))=
, f4(x)=f(f3(x))= ……根据以上事实,由归纳推理可得:当n∈N*, n≥2时,fn(x)=f(n-1(x))= .
……根据以上事实,由归纳推理可得:当n∈N*, n≥2时,fn(x)=f(n-1(x))= . ,则输出的
,则输出的 的值为____.
的值为____.
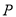 为曲线
为曲线 上任意一点,O为坐标原点,则
上任意一点,O为坐标原点,则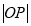 的最小值为
的最小值为 B.
B. C.
C. D.
D.
 在
在 上有意义,则实数
上有意义,则实数 的取值范围为
的取值范围为 B.
B.  C.
C.  D.
D. 
 ,则目标函数
,则目标函数 的最大值为 .
的最大值为 .  的图像是
的图像是 

 ;②
;②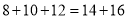 ;
;
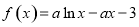 (
( ).
). 的单调性;
的单调性;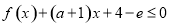 对任意
对任意 恒成立,求实数
恒成立,求实数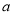 的取值范围(
的取值范围(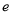 为自然常数);
为自然常数);
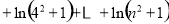

 (
( ,
, ).
).