题目内容

如图所示，F1、F2分别为椭圆C：的左、右两个焦点，A、B为两个顶点，已知椭圆C上的点（1，）到F1、F2 两点的距离之和为4。

       （1）求椭圆C的方程和焦点坐标；

       （2）过椭圆C的焦点F2作AB的平行线交椭圆于P、Q两点，求△F1PQ的面积。

解：（1）由题设知：，即                                   

将点（1，）代入椭圆方程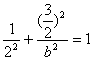

解得                                                                 

∴                      

故椭圆方程为                                   

焦点F1、F2的坐标分别为（－1，0）和（1，0）  

（2）由（1）知，A（－2，0），B（0，）

∴                          

∴PQ所在直线方程为

       由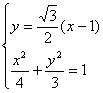，得

                                                     

       设P（，），Q（，），则

       ，                             

       ∴ 

       ∴。

练习册系列答案
相关题目
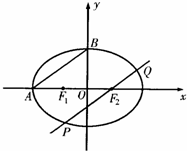精英家教网如图所示，F1，F2分别为椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的左、右两个焦点，A，B为两个顶点，已知椭圆C上的点到F1，F2两点的距离之和为4且b=
3
．
（1）求椭圆C的方程和焦点坐标；
（2）过椭圆C的焦点F2作AB的平行线交椭圆于P，Q两点，求△F1PQ的面积．
精英家教网如图所示，F1、F2分别为椭圆C：
x2
a2
+
y2
b2
=1 (a＞b＞0)的左、右两个焦点，A、B为两个顶点，已知椭圆C上的点(1，
3
2
)到F1、F2两点的距离之和为4．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过椭圆C的焦点F2作AB的平行线交椭圆于P、Q两点，求△F1PQ的面积．
如图所示，F1、F2分别为椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右两个焦点，A、B为两个顶点，已知椭圆C上的点（1，
3
2
）到F1、F2两点的距离之和为4．
（1）求椭圆C的方程和焦点坐标；
（2）设点M是椭圆上的动点N（0，
1
2
），求|MN|的最大值．
（3）过椭圆C的焦点F2作AB的平行线交椭圆于P、Q两点，求△F1PQ的面积．
如图所示，F1、F2分别为椭圆C：
x2
a2
+
y2
b2
=1 (a＞b＞0)的左、右两个焦点，A、B为两个顶点；已知顶点B(0，
3
)到F1、F2两点的距离之和为4．
（1）求椭圆C的方程；
（2）证明：椭圆C上任意一点M（x0，y0）到右焦点F2的距离的最小值为1．
（3）作AB的平行线交椭圆C于P、Q两点，求弦长|PQ|的最大值，并求|PQ|取最大值时△F1PQ的面积．
（2013•牡丹江一模）如图所示，F1和F2分别是双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的两个焦点，A和B是以O为圆心，|OF1|为半径的圆与该双曲线左支的两个交点，且△F2AB是等边三角形，则离心率为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网