题目内容
已知圆O的半径为4,直径AB上一点D使 ,E、F为另一直径的两个端点,则
,E、F为另一直径的两个端点,则 =( )
=( )A.-10
B.-11
C.-12
D.-16
【答案】分析:由已知中圆C的半径为3,直径AB上一点D使 ,我们可以求出向量
,我们可以求出向量  ,
, ,
, 的模,取EF为垂直AB,则可进一步求出向量
的模,取EF为垂直AB,则可进一步求出向量 、
、 的模,及∠EDF的余弦值,代入向量数量积公式,即可得到答案.
的模,及∠EDF的余弦值,代入向量数量积公式,即可得到答案.
解答:解:圆C的半径为3,直径AB上一点D使 ,我们可以求出|
,我们可以求出| |=8,|
|=8,| |=2,|
|=2,| |=2.
|=2.
取EF为垂直AB,则可进一步求出| |=
|= =|
=| |.
|.
由于∠EDF=2∠EDO,又∵cos∠EDO= =
= =
= ,
,
∴cos∠EDF=cos2∠EDO=2× -1=-
-1=- ,
,
∴ =
= cos∠EDF=20×(-
cos∠EDF=20×(- )=-12,
)=-12,
故选C.
点评:本题考查的知识点是平面向量的数量积的运算,直线与圆相交的性质,考虑到本题是一个选择题,我们可以用特殊值法解答本题,属于中档题.
 ,我们可以求出向量
,我们可以求出向量  ,
, ,
, 的模,取EF为垂直AB,则可进一步求出向量
的模,取EF为垂直AB,则可进一步求出向量 、
、 的模,及∠EDF的余弦值,代入向量数量积公式,即可得到答案.
的模,及∠EDF的余弦值,代入向量数量积公式,即可得到答案.解答:解:圆C的半径为3,直径AB上一点D使
 ,我们可以求出|
,我们可以求出| |=8,|
|=8,| |=2,|
|=2,| |=2.
|=2.取EF为垂直AB,则可进一步求出|
 |=
|= =|
=| |.
|.由于∠EDF=2∠EDO,又∵cos∠EDO=
 =
= =
= ,
,∴cos∠EDF=cos2∠EDO=2×
 -1=-
-1=- ,
,∴
 =
= cos∠EDF=20×(-
cos∠EDF=20×(- )=-12,
)=-12,故选C.
点评:本题考查的知识点是平面向量的数量积的运算,直线与圆相交的性质,考虑到本题是一个选择题,我们可以用特殊值法解答本题,属于中档题.

练习册系列答案
相关题目
 ,E、F为另一直径的两个端点,则
,E、F为另一直径的两个端点,则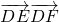 =
= ,E、F为另一直径的两个端点,则
,E、F为另一直径的两个端点,则 =( )
=( )