题目内容
如图,在平面直角坐标系 中,点A(0,3),直线
中,点A(0,3),直线 :
: ,设圆
,设圆 的半径为1,圆心在
的半径为1,圆心在 上.
上.

(1)若圆心 也在直线
也在直线 上,过点A作圆
上,过点A作圆 的切线,求切线的方程;
的切线,求切线的方程;
(2)若圆 上存在点
上存在点 ,使
,使 ,求圆心
,求圆心 的横坐标
的横坐标 的取值范围.
的取值范围.
(1) 和
和 ;(2)
;(2)
【解析】
试题分析:(1)联立直线l与直线y=x-1解析式,求出方程组的解得到圆心C坐标,根据A坐标设出切线的方程,由圆心到切线的距离等于圆的半径,列出关于k的方程,求出方程的解得到k的值,确定出切线方程即可;(2)设M(x,y),由MA=2MO,利用两点间的距离公式列出关系式,整理后得到点M的轨迹为以(0,-1)为圆心,2为半径的圆,可记为圆D,由M在圆C上,得到圆C与圆D相交或相切,根据两圆的半径长,得出两圆心间的距离范围,利用两点间的距离公式列出不等式,求出不等式的解集,即可得到a的范围.
试题解析:联立 和
和 可得圆心
可得圆心 (3,2),又因为半径为1,
(3,2),又因为半径为1,
所以圆 的方程为
的方程为 ,
,
设过点A的切线方程为: ,
,
圆心到直线的距离为
所以 或
或
所求切线方程为 和
和 。
。
(2)设点
因为
所以

又因为点 在圆
在圆 上,
上,
所以圆 与圆
与圆 相交,
相交,
设点
两圆圆心距满足: , 所以
, 所以 .
.
考点:点线距离公式,圆与圆的位置关系,圆的切线公式

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
 ,
, ,则集合
,则集合 = .
= . 中,
中, ,
, ,
, ,则
,则 边上的高为( )
边上的高为( ) B.
B.
 D.
D.
 人,其年龄统计表如下:由于电脑故障,有两个数字在表格中不能显示出来,则下列说法正确的是( )
人,其年龄统计表如下:由于电脑故障,有两个数字在表格中不能显示出来,则下列说法正确的是( )
 ,众数是
,众数是

 和
和
 和
和
 和
和
 和
和
 R),则ab=
R),则ab=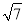 ,BC=2,B=60°,则BC边上的高等于( )
,BC=2,B=60°,则BC边上的高等于( )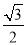 B.
B.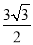 C.
C.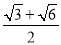 D.
D.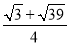

 B.
B. C.
C. D.
D.
 的图象向右平移
的图象向右平移 个单位长度后得到函数
个单位长度后得到函数 的图象,若
的图象,若 的图象都经过点
的图象都经过点 ,则
,则 的值可以是
的值可以是 B.
B. C.
C. D.
D.