题目内容
(本题满分16分)如图,在平面直角坐标系 中,离心率为
中,离心率为 的椭圆
的椭圆
 的左顶点为
的左顶点为 ,过原点
,过原点 的直线(与坐标轴不重合)与椭圆
的直线(与坐标轴不重合)与椭圆 交于
交于 两点,直线
两点,直线 分别与
分别与 轴交于
轴交于 两点.若直线
两点.若直线 斜率为
斜率为 时,
时, .
.

(1)求椭圆 的标准方程;
的标准方程;
(2)试问以 为直径的圆是否经过定点(与直线
为直径的圆是否经过定点(与直线 的斜率无关)?请证明你的结论.
的斜率无关)?请证明你的结论.
(1) (2)过定点
(2)过定点 .
.
【解析】
试题分析:(1)因为离心率为 ,所以要确定椭圆标准方程,只需再确定一个独立条件,即点P坐标:根据点
,所以要确定椭圆标准方程,只需再确定一个独立条件,即点P坐标:根据点 斜率为
斜率为 且
且 可求
可求 ,所以
,所以 ,又
,又 ,解得椭圆
,解得椭圆 的标准方程为
的标准方程为 .(2)用点P坐标表示出
.(2)用点P坐标表示出 的坐标及以
的坐标及以 为直径的圆的方程:设
为直径的圆的方程:设 ,则直线
,则直线 方程为:
方程为: ,∴
,∴ ,直线
,直线 方程为:
方程为: ,∴
,∴ ,以
,以 为直径的圆为
为直径的圆为 ,利用
,利用 化简得
化简得 ,所以动圆必过
,所以动圆必过 与
与 的交点
的交点
试题解析:【解析】
(1)设 ,
,
∵直线 斜率为
斜率为 时,
时, ,∴
,∴ ,∴
,∴ 3分
3分
∴ ,∵
,∵ ,∴
,∴ .
.
∴椭圆 的标准方程为
的标准方程为 . 6分
. 6分
(2)以 为直径的圆过定点
为直径的圆过定点 .
.
设 ,则
,则 ,且
,且 ,即
,即 ,
,
∵ ,∴直线
,∴直线 方程为:
方程为: ,∴
,∴ ,
,
直线 方程为:
方程为: ,∴
,∴ , 9分
, 9分
以 为直径的圆为
为直径的圆为
即 , 12分
, 12分
∵ ,∴
,∴ ,
,
令 ,
, ,解得
,解得 ,
,
∴以 为直径的圆过定点
为直径的圆过定点 . 16分
. 16分
考点:直线与椭圆位置关系
考点分析: 考点1:椭圆的标准方程 考点2:椭圆的几何性质 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 )(x∈R).
)(x∈R). )=
)= ,α∈(
,α∈( ),求cosα的值.
),求cosα的值. .
. ,求
,求 在
在 上的最大值和最小值;
上的最大值和最小值; 的值.
的值. ,若f(x)的值域为R,是实数a的取值范围是
,若f(x)的值域为R,是实数a的取值范围是
 ”,命题P的否定:
”,命题P的否定:
 中,角
中,角 所对的边分别为
所对的边分别为 ,若
,若 且
且 ,则
,则 的方差为
的方差为 ,则
,则 .
. 中,角
中,角 的终边经过点
的终边经过点 .
. 的值;
的值; 关于
关于 轴的对称点为
轴的对称点为 ,求
,求 的值.
的值.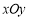 中,已知圆
中,已知圆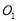 ,圆
,圆 均与
均与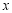 轴相切且圆心
轴相切且圆心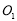 ,
,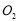 与原点
与原点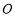 共线,
共线,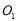 ,
,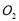 两点的横坐标之积为6,设圆
两点的横坐标之积为6,设圆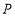 ,
,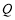 两点,直线
两点,直线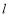 :
: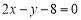 ,则点
,则点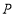 与直线
与直线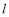 上任意一点
上任意一点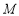 之间的距离的最小值为 .
之间的距离的最小值为 .