题目内容
设e为自然对数的底数,已知直线l:y=-e-t(x-t)+e-t,t>-1,则直线l与两条坐标轴所围成的三角形面积的最大值等于
.
| 2 |
| e |
| 2 |
| e |
分析:分别令x=0与y=0可求得l与两条坐标轴的交点坐标,于是可得到所围成的三角形面积的表达式,继而可利用导数法求其最大值.
解答:解:∵直线l:y=-e-t(x-t)+e-t,
令x=0,y=(t+1)e-t,即A(0,(t+1)e-t)
令y=0,x=t+1,故B(t+1,0),
∵t>-1,
∴S△OAB=
|t+1|•|t+1|e-t=
(t2+2t+1)e-t,
∴S′△OAB=
(2t+2)e-t+
(t2+2t+1)e-t×(-1)=
e-t(1-t2),
∵t>-1,
∴当t=1时,S′△OAB=0,
当t>1时,S′△OAB<0,当-1<t<1时,S′△OAB,>0,
∴当t=1时,S△OAB有极大值,
∵S′△OAB=0的t的值唯一,
∴S△OAB的极大值就是最大值.
∴当t=1时,S△OAB有最大值,
S△OAB的最大值为
×(1+1)(1+1)e-1=
.
故答案为:
.
令x=0,y=(t+1)e-t,即A(0,(t+1)e-t)
令y=0,x=t+1,故B(t+1,0),
∵t>-1,
∴S△OAB=
| 1 |
| 2 |
| 1 |
| 2 |
∴S′△OAB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵t>-1,
∴当t=1时,S′△OAB=0,
当t>1时,S′△OAB<0,当-1<t<1时,S′△OAB,>0,
∴当t=1时,S△OAB有极大值,
∵S′△OAB=0的t的值唯一,
∴S△OAB的极大值就是最大值.
∴当t=1时,S△OAB有最大值,
S△OAB的最大值为
| 1 |
| 2 |
| 2 |
| e |
故答案为:
| 2 |
| e |
点评:本题考查直线的一般式方程,考查三角形面积的表达式及其应用,考查导数法求最值中的应用,属于中档题.

练习册系列答案
相关题目
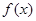 的最大值;
的最大值; 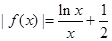 是否有实数解 .
是否有实数解 . =
= 是否有实数解.
是否有实数解.