题目内容
(2013•楚雄州模拟)已知函数f(x)=ax+lnx,其中a为常数,设e为自然对数的底数.
(1)当a=-1时,求f(x)的最大值;
(2)若f(x)在区间(0,e]上的最大值为-3,求a的值;
(3)当a=-1时,试推断方程|f(x)|=
+
是否有实数解.
(1)当a=-1时,求f(x)的最大值;
(2)若f(x)在区间(0,e]上的最大值为-3,求a的值;
(3)当a=-1时,试推断方程|f(x)|=
| lnx |
| x |
| 1 |
| 2 |
分析:(1)在定义域(0,+∞)内对函数f(x)求导,求其极大值,若是唯一极值点,则极大值即为最大值.
(2)在定义域(0,+∞)内对函数f(x)求导,对a进行分类讨论并判断其单调性,根据f(x)在区间(0,e]上的单调性求其最大值,并判断其最大值是否为-3,若是就可求出相应的最大值.
(3)根据(1)可求出|f(x)|的值域,通过求导可求出函数g(x)═
+
的值域,通过比较上述两个函数的值域,就可判断出方程|f(x)|=
+
是否有实数解.
(2)在定义域(0,+∞)内对函数f(x)求导,对a进行分类讨论并判断其单调性,根据f(x)在区间(0,e]上的单调性求其最大值,并判断其最大值是否为-3,若是就可求出相应的最大值.
(3)根据(1)可求出|f(x)|的值域,通过求导可求出函数g(x)═
| lnx |
| x |
| 1 |
| 2 |
| lnx |
| x |
| 1 |
| 2 |
解答:解:(1)易知f(x)定义域为(0,+∞),
当a=-1时,f(x)=-x+lnx,f′(x)=-1+
=
,令f′(x)=0,得x=1.
当0<x<1时,f′(x)>0;当x>1时,f′(x)<0.
∴f(x)在(0,1)上是增函数,在(1,+∞)上是减函数.
f(x)max=f(1)=-1.
∴函数f(x)在(0,+∞)上的最大值为-1.
(2)∵f′(x)=a+
,x∈(0,e],
∈[
,+∞).
①若a≥-
,则f′(x)≥0,从而f(x)在(0,e]上增函数,
∴f(x)max=f(e)=ae+1≥0,不合题意.
②若a<-
,则由f′(x)>0⇒a+
>0,即0<x<-
由f′(x)<0⇒a+
<0,即-
<x≤e.
从而f(x)在(0,-
)上增函数,在(-
,e)为减函数
∴f(x)max=f(-
)=-1+ln(-
)
令-1+ln(-
)=-3,则ln(-
)=-2
∴-
=e-2,即a=-e2.∵-e2<-
,∴a=-e2为所求.
(3)由(1)知当a=-1时f(x)max=f(1)=-1,
∴|f(x)|≥1.
又令g(x)=
+
,g′(x)=
,令g′(x)=0,得x=e,
当0<x<e时,g′(x)>0,g(x) 在(0,e)单调递增;
当x>e时,g′(x)<0,g(x) 在(e,+∞)单调递减.
∴g(x)max=g(e)=
+
<1,∴g(x)<1,
∴|f(x)|>g(x),即|f(x)|>
+
.
∴方程|f(x)|=
+
没有实数解.
当a=-1时,f(x)=-x+lnx,f′(x)=-1+
| 1 |
| x |
| 1-x |
| x |
当0<x<1时,f′(x)>0;当x>1时,f′(x)<0.
∴f(x)在(0,1)上是增函数,在(1,+∞)上是减函数.
f(x)max=f(1)=-1.
∴函数f(x)在(0,+∞)上的最大值为-1.
(2)∵f′(x)=a+
| 1 |
| x |
| 1 |
| x |
| 1 |
| e |
①若a≥-
| 1 |
| e |
∴f(x)max=f(e)=ae+1≥0,不合题意.
②若a<-
| 1 |
| e |
| 1 |
| x |
| 1 |
| a |
由f′(x)<0⇒a+
| 1 |
| x |
| 1 |
| a |
从而f(x)在(0,-
| 1 |
| a |
| 1 |
| a |
∴f(x)max=f(-
| 1 |
| a |
| 1 |
| a |
令-1+ln(-
| 1 |
| a |
| 1 |
| a |
∴-
| 1 |
| a |
| 1 |
| e |
(3)由(1)知当a=-1时f(x)max=f(1)=-1,
∴|f(x)|≥1.
又令g(x)=
| lnx |
| x |
| 1 |
| 2 |
| 1-lnx |
| x2 |
当0<x<e时,g′(x)>0,g(x) 在(0,e)单调递增;
当x>e时,g′(x)<0,g(x) 在(e,+∞)单调递减.
∴g(x)max=g(e)=
| 1 |
| e |
| 1 |
| 2 |
∴|f(x)|>g(x),即|f(x)|>
| lnx |
| x |
| 1 |
| 2 |
∴方程|f(x)|=
| lnx |
| x |
| 1 |
| 2 |
点评:本题先通过对函数求导,求其极值,进而在求其最值及值域,用到分类讨论的思想方法.

练习册系列答案
相关题目
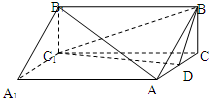 (2013•楚雄州模拟)如图,三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,AC=BC=2,AA1=3,D为AC的中点.
(2013•楚雄州模拟)如图,三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,AC=BC=2,AA1=3,D为AC的中点.