题目内容
设数列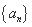 的前
的前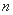 项和为
项和为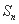 ,并且满足
,并且满足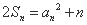 ,
,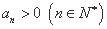 .
.
(Ⅰ) 求 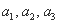 ;
;
(Ⅱ)猜想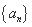 的通项公式,并用数学归纳法加以证明.
的通项公式,并用数学归纳法加以证明.
解:分别令n=1,2,3,得
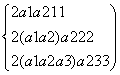
∵an>0,∴a1=1,a2=2,a3=3.
(2)解 猜想:an=n, 由2Sn=a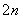 +n, ①
+n, ①
可知,当n≥2时,2Sn-1=a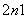 +(n-1), ②
+(n-1), ②
①-②,得2an=a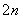 -a
-a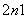 +1,即a
+1,即a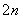 =2an+a
=2an+a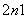 -1. (ⅰ)当n=2时,a
-1. (ⅰ)当n=2时,a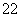 =2a2+12-1,∵a2>0,∴a2=2;
=2a2+12-1,∵a2>0,∴a2=2;
(ⅱ)假设当n=k(k≥2)时,ak=k.
那么当n=k+1时,
[ak+1-(k+1)][ak+1+(k-1)]=0,
∵ak+1>0,k≥2,∴ak+1+(k-1)>0,
∴ak+1=k+1.
这就是说,当n=k+1时也成立,
∴an=n(n≥2).显然n=1时,也适合.
综合(1)(2)可知对于n∈N*,an=n都成立。

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
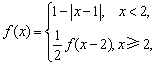 则函数
则函数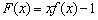 的零点的个数为 .
的零点的个数为 .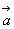 ,
,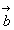 的夹角为30°,
的夹角为30°, ,
,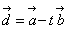 .若
.若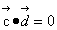 ,则正实数
,则正实数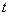 =____________
=____________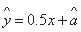 ,据此模型预报身高为
,据此模型预报身高为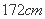 的男生的体重大约为( )
的男生的体重大约为( )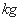 B.70
B.70 
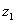 ,
, 在复平面内的对应点关于实轴对称,
在复平面内的对应点关于实轴对称,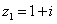 ,则
,则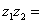 ( )
( )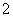 B.
B.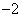 C.
C. D.
D.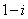
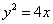 与双曲线
与双曲线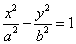 (
(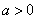 ,
,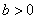 )有相同的焦点
)有相同的焦点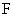 ,点
,点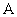 是两曲线的一个交点,且
是两曲线的一个交点,且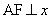 轴,则双曲线的离心率是( )
轴,则双曲线的离心率是( )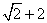 B.
B.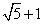 C.
C.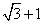 D.
D.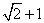
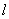 是直线,
是直线,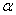 ,
,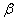 为两个不同的平面,下列说法正确的是( )
为两个不同的平面,下列说法正确的是( )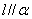 ,
,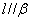 ,则
,则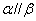 B.若
B.若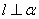 ,
,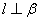 ,则
,则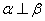 ,
,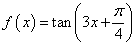 .
.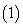 求
求 的值;
的值; 若
若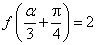 ,求
,求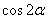 的值.
的值.