题目内容
设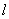 是直线,
是直线,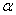 ,
,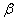 为两个不同的平面,下列说法正确的是( )
为两个不同的平面,下列说法正确的是( )
A.若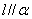 ,
,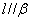 ,则
,则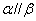 B.若
B.若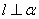 ,
,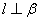 ,则
,则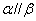
C.若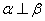 ,
,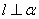 ,则
,则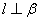 D.若
D.若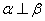 ,
,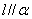 ,则
,则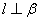
B

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
题目内容
设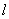 是直线,
是直线,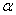 ,
,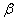 为两个不同的平面,下列说法正确的是( )
为两个不同的平面,下列说法正确的是( )
A.若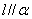 ,
,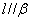 ,则
,则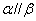 B.若
B.若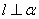 ,
,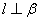 ,则
,则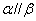
C.若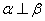 ,
,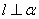 ,则
,则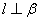 D.若
D.若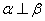 ,
,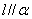 ,则
,则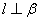
B

 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案