题目内容
(本小题满分14分)已知数列 满足
满足 ,
, ,
, .
.
(1)求证:数列 是等差数列;
是等差数列;
(2)求证: .
.
见解析
【解析】
试题解析:证明:(1)∵ ,
,
∴ ,
,
∴ 3 分
3 分
∴ 数列{ }是以
}是以 为首项,以1为公差的等差数列. 5 分
为首项,以1为公差的等差数列. 5 分
证法 2:由已知
即 ,
,
即 (常数) 3 分
(常数) 3 分
∴ 数列{ }是以
}是以 为首项,以1为公差的等差数列. 5分
为首项,以1为公差的等差数列. 5分
(2)由(1)得 ,
,
所以 , 6分
, 6分
一方面, ∵ 7 分
7 分
∴  ? 9分
? 9分
另一方面, ∵ 11分
11分
∴ 
 ? 13分
? 13分
故不等式 成立. 14 分
成立. 14 分
考点:考查了等差数列,数列与不等式的综合应用.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 B.
B.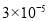 C.
C.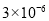 D.
D.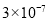
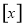 表示不超过
表示不超过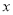 的最大整数,例如
的最大整数,例如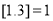 ,
,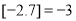 .函数
.函数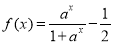
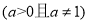 ,在
,在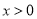 时恒有
时恒有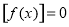 ,则实数
,则实数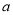 的取值范围是( )
的取值范围是( )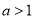 B.
B.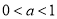 C.
C.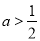 D.
D.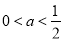
 B.
B. C.
C. D.
D.
 上的动点
上的动点 到直线
到直线 的距离最小值是 .
的距离最小值是 .
 B.
B. C.
C. D.
D.
 在点
在点 处的切线方程为 .
处的切线方程为 . ,则
,则 __________.
__________.