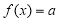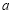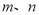题目内容
已知函数 的图象过点(2,0).
的图象过点(2,0).
⑴求m的值;
⑵证明 的奇偶性;
的奇偶性;
⑶判断 在
在 上的单调性,并给予证明;
上的单调性,并给予证明;
(1)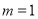 ;(2)
;(2)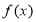 是奇函数;(3)
是奇函数;(3)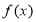 在
在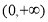 上为单调增函数.
上为单调增函数.
【解析】
试题分析:(1)由已知可将点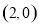 代入函数
代入函数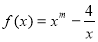 ,得
,得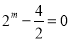 ,从而求出
,从而求出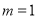 ;(2)根据函数奇偶性的定义可证明(定义法证明函数的奇偶性的步骤:①先判断定义域是否关于原点对称;②再判断
;(2)根据函数奇偶性的定义可证明(定义法证明函数的奇偶性的步骤:①先判断定义域是否关于原点对称;②再判断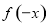 与
与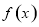 的关系,即若
的关系,即若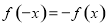 则为奇函数,若
则为奇函数,若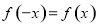 则为偶函数).由(1)得函数
则为偶函数).由(1)得函数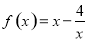 ,其定义为
,其定义为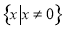 关于原点对称,又
关于原点对称,又 ,所以函数
,所以函数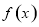 为奇函数;(3)根据函数单调性的定义可判断(定义法判断函数的单调性一般步骤为:①在其定义域内任取两个自变量
为奇函数;(3)根据函数单调性的定义可判断(定义法判断函数的单调性一般步骤为:①在其定义域内任取两个自变量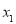 、
、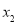 ,且
,且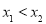 ;②作差(或作商)比较
;②作差(或作商)比较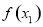 与
与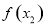 的大小;③得出结论,即若
的大小;③得出结论,即若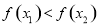 则为单调递增函数,若
则为单调递增函数,若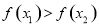 则为单调递减函数).
则为单调递减函数).
试题解析:⑴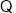
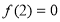 ,∴
,∴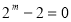 ,
,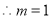 . 2分
. 2分
⑵因为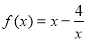 ,定义域为
,定义域为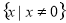 ,关于原点成对称区间. 3分
,关于原点成对称区间. 3分
又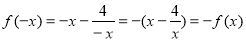 ,
,
所以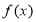 是奇函数. 6分
是奇函数. 6分
⑶设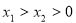 ,则
,则
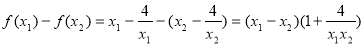 8分
8分
因为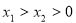 ,所以
,所以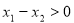 ,
,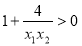 ,
,
所以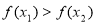 ,因此,
,因此,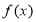 在
在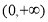 上为单调增函数. 10分
上为单调增函数. 10分
考点:函数的解析式、奇偶性、单调性

练习册系列答案
相关题目