题目内容

设a是f(x)=
1
x
-lnx的零点，若0＜x0＜a，则f（x0）的值满足（　　）
分析：利用导数判断函数的单调性，再根据函数零点的定义即可得出．
解答：解：∵x＞0，∴f′(x)=-
1
x2
-
1
x
＜0，∴函数f（x）在（0，+∞）上单调递减．
又∵f（a）=0，0＜x0＜a，∴f（x0）＞f（a）=0．
故选C．
点评：熟练掌握利用导数判断函数的单调性和函数零点的定义是解题的关键．
练习册系列答案
相关题目
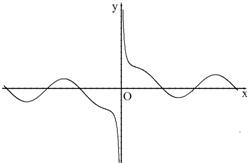精英家教网如图是函数Q（x）的图象的一部分，设函数f（x）=sinx，g （ x ）=
1
x
，则Q（x）是（　　）
A、
f(x)
g(x)
B、f（x）g（x）
C、f（x）-g（x）
D、f（x）+g（x）
（2009•临沂一模）设f（x）是连续的偶函数，且当x＞0时是单调函数，则满足f(2x)=f(
x+1
x+4
)的所有x之和为（　　）
（2009•大连二模）（I）已知函数f（x）=x-
1
x
，x∈(
1
4
，
1
2
)，P(x1，f(x1))，Q(x2，f(x2))是f(x)图象上的任意两点，且x1＜x2．
①求直线PQ的斜率kPQ的取值范围及f（x）图象上任一点切线的斜率k的取值范围；
②由①你得到的结论是：若函数f（x）在[a，b]上有导函数f′（x），且f（a）、f（b）存在，则在（a，b）内至少存在一点ξ，使得f′（ξ）=
f(b)-f(a)
b-a
f(b)-f(a)
b-a
成立（用a，b，f（a），f（b）表示，只写出结论，不必证明）
（II）设函数g（x）的导函数为g′（x），且g′（x）为单调递减函数，g（0）=0．试运用你在②中得到的结论证明：
当x∈（0，1）时，f（1）x＜g（x）．
设函数f(x)=
1
x
，则f（x）是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网