题目内容
【题目】无穷数列![]() 满足:
满足:![]() 为正整数,且对任意正整数
为正整数,且对任意正整数![]() ,
,![]() 为前
为前![]() 项
项![]() 、
、![]() 、
、![]() 、
、![]() 中等于
中等于![]() 的项的个数.
的项的个数.
(1)若![]() ,求
,求![]() 和
和![]() 的值;
的值;
(2)已知命题![]() 存在正整数
存在正整数![]() ,使得
,使得![]() ,判断命题
,判断命题![]() 的真假并说明理由;
的真假并说明理由;
(3)若对任意正整数![]() ,都有
,都有![]() 恒成立,求
恒成立,求![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ;(2)真命题,证明见解析;(3)
;(2)真命题,证明见解析;(3)![]() .
.
【解析】
(1)根据题意直接写出![]() 、
、![]() 、
、![]() 的值,可得出结果;
的值,可得出结果;
(2)分![]() 和
和![]() 两种情况讨论,找出使得等式
两种情况讨论,找出使得等式![]() 成立的正整数
成立的正整数![]() ,可得知命题
,可得知命题![]() 为真命题;
为真命题;
(3)先证明出“![]() ”是“存在
”是“存在![]() ,当
,当![]() 时,恒有
时,恒有![]() 成立”的充要条件,由此可得出
成立”的充要条件,由此可得出![]() ,然后利用定义得出
,然后利用定义得出![]() ,由此可得出
,由此可得出![]() 的值.
的值.
(1)根据题意知,对任意正整数![]() ,
,![]() 为前
为前![]() 项
项![]() 、
、![]() 、
、![]() 、
、![]() 中等于
中等于![]() 的项的个数,
的项的个数,
因此,![]() ,
,![]() ,
,![]() ;
;
(2)真命题,证明如下:
①当![]() 时,则
时,则![]() ,
,![]() ,
,![]() ,此时,当
,此时,当![]() 时,
时,![]() ;
;
②当![]() 时,设
时,设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
此时,当![]() 时,
时,![]() .
.
综上所述,命题![]() 为真命题;
为真命题;
(3)先证明:“![]() ”是“存在
”是“存在![]() ,当
,当![]() 时,恒有
时,恒有![]() 成立”的充要条件.
成立”的充要条件.
假设存在![]() ,使得“存在
,使得“存在![]() ,当
,当![]() 时,恒有
时,恒有![]() 成立”.
成立”.
则数列![]() 的前
的前![]() 项为
项为![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
后面的项顺次为![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
故对任意的![]() ,
,![]()
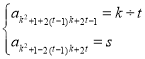 ,
,
对任意的![]() ,取
,取![]() ,其中
,其中![]() 表示不超过
表示不超过![]() 的最大整数,则
的最大整数,则![]() ,
,
令![]() ,则
,则![]() ,此时
,此时![]() ,
,![]()
有![]() ,这与
,这与![]() 矛盾,
矛盾,
故若存在![]() ,当
,当![]() 时,恒有
时,恒有![]() 成立,必有
成立,必有![]() ;从而得证.
;从而得证.
另外:当![]() 时,数列
时,数列![]() 为
为![]() ,
,
故![]() ,则
,则![]() .
.

练习册系列答案
相关题目
【题目】在某次测试中,卷面满分为![]() 分,考生得分为整数,规定
分,考生得分为整数,规定![]() 分及以上为及格.某调研课题小组为了调查午休对考生复习效果的影响,对午休和不午休的考生进行了测试成绩的统计,数据如下表:
分及以上为及格.某调研课题小组为了调查午休对考生复习效果的影响,对午休和不午休的考生进行了测试成绩的统计,数据如下表:
分数段 |
|
|
|
|
|
|
|
午休考生人数 | 29 | 34 | 37 | 29 | 23 | 18 | 10 |
不午休考生人数 | 20 | 52 | 68 | 30 | 15 | 12 | 3 |
(1)根据上述表格完成下列列联表:
及格人数 | 不及格人数 | 合计 | |
午休 | |||
不午休 | |||
合计 |
(2)判断“能否在犯错误的概率不超过![]() 的前提下认为成绩及格与午休有关”?
的前提下认为成绩及格与午休有关”?
| 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)




