Question

在平面直角坐标系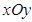中，已知双曲线.

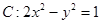 （1）设F是C的左焦点，M是C右支上一点. 若|MF|=2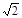，求过M点的坐标；（5分）

（2）过C的左顶点作C的两条渐近线的平行线，求这两组平行线围成的平行四边形的

面积；（5分）

    （3）设斜率为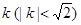的直线l2交C于P、Q两点，若l与圆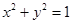相切，

求证：OP⊥OQ；（6分）

 

Answer 1

【答案】

（1）；（2）；（3）见解析.

【解析】（1）双曲线，左焦点.

         设，则，       ……2分

         由M是右支上一点，知，所以，得.

         所以.                                       ……5分

    （2）左顶点，渐近线方程：.

         过A与渐近线平行的直线方程为：，即.

         解方程组，得.                      ……8分

         所求平行四边形的面积为.                   ……10分

   （3）设直线PQ的方程是.因直线与已知圆相切，故，

即 (*).

由，得.

        设P(x1, y1)、Q(x2, y2)，则.

        ，所以

       

         .

         由(*)知，所以OP⊥OQ.                      ……16分