题目内容
 如图,直线y=2x与抛物线y=3-x2所围成的阴影部分的面积是
如图,直线y=2x与抛物线y=3-x2所围成的阴影部分的面积是
- A.

- B.

- C.

- D.

D
分析:联解方程组,得直线与抛物线交于点A(-3,-6)和B(1,2),因此求出函数3-x2-2x在区间[-3,1]上的定积分值,就等于所求阴影部分的面积,接下来利用积分计算公式和法则进行运算,即可得到本题的答案.
解答: 由
由 ,解得
,解得 或
或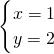
∴直线y=2x与抛物线y=3-x2交于点A(-3,-6)和B(1,2)
∴两图象围成的阴影部分的面积为

=(3×1- ×13-12)-[3×(-3)-
×13-12)-[3×(-3)- ×(-3)3-(-3)2]
×(-3)3-(-3)2]
= ,
,
故选:D
点评:本题求直线与抛物线围成的阴影部分图形的面积,着重考查了定积分计算公式和定积分的几何意义等知识,属于基础题.
分析:联解方程组,得直线与抛物线交于点A(-3,-6)和B(1,2),因此求出函数3-x2-2x在区间[-3,1]上的定积分值,就等于所求阴影部分的面积,接下来利用积分计算公式和法则进行运算,即可得到本题的答案.
解答:
 由
由 ,解得
,解得 或
或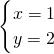
∴直线y=2x与抛物线y=3-x2交于点A(-3,-6)和B(1,2)
∴两图象围成的阴影部分的面积为

=(3×1-
 ×13-12)-[3×(-3)-
×13-12)-[3×(-3)- ×(-3)3-(-3)2]
×(-3)3-(-3)2]=
 ,
,故选:D
点评:本题求直线与抛物线围成的阴影部分图形的面积,着重考查了定积分计算公式和定积分的几何意义等知识,属于基础题.

练习册系列答案
相关题目
 (2013•南开区二模)如图,直线y=2x与抛物线y=3-x2所围成的阴影部分的面积是( )
(2013•南开区二模)如图,直线y=2x与抛物线y=3-x2所围成的阴影部分的面积是( ) 如图,直线y=2x与抛物线y=3-x2所围成的阴影部分的面积是( )
如图,直线y=2x与抛物线y=3-x2所围成的阴影部分的面积是( )



 如图,直线y=2x与抛物线y=3-x2所围成的阴影部分的面积是( )
如图,直线y=2x与抛物线y=3-x2所围成的阴影部分的面积是( )



 如图,直线y=2x与抛物线y=3-x2所围成的阴影部分的面积是( )
如图,直线y=2x与抛物线y=3-x2所围成的阴影部分的面积是( )


