题目内容
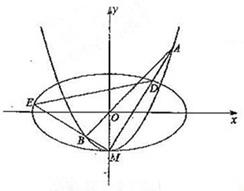
如图,椭圆C1: +y2=1,x轴被曲线C2:y=x2-b截得的线段长等于C1的长半轴长.
+y2=1,x轴被曲线C2:y=x2-b截得的线段长等于C1的长半轴长.(1)求实数b的值;
(2)设C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A、B,直线MA、MB分别与C1相交与D、E.
①证明:MD•ME=0;
②记△MAB,△MDE的面积分别是S1,S2.若
 =λ,求λ的取值范围.
=λ,求λ的取值范围.
【答案】分析:(1)确定半长轴为2,利用x轴被曲线C2:y=x2-b截得的线段长等于C1的长半轴长,可求b的值;
(2)①设直线的方程与抛物线方程联立,利用点M的坐标为(0,-1),可得kMAkMB=-1,从而得证;
②设直线的斜率为k1,则直线的方程为y=k1x-1,代入抛物线方程可得x2=k1x,从而可得点A的坐标、点B的坐标,进而可得S1,同理可得S2,进而可得比值,由此可得λ的取值范围.
解答:(1)解:由题意知:半长轴为2,则有2 =2 …(3分)
=2 …(3分)
∴b=1 …(4分)
(2)①证明:由题意知,直线l的斜率存在,设为k,则直线的方程为y=kx.
与抛物线方程联立,消去y可得x2-kx-1=0,…(6分)
设A(x1,y1),B(x2,y2),则x1,x2是上述方程的两个实根,于是x1+x2=k,x1x2=-1.…(7分)
又点M的坐标为(0,-1),所以kMAkMB= ×
× =
= =-1…(9分)
=-1…(9分)
故MA⊥MB,即MD⊥ME,故 …(10分)
…(10分)
②设直线的斜率为k1,则直线的方程为y=k1x-1,代入抛物线方程可得x2=k1x,解得x=0或x=k1,则点A的坐标为(k1, ) …(12分)
) …(12分)
同理可得点B的坐标为 .
.
于是 =
= =
=
直线的方程为y=k1x-1,代入椭圆方程,消去y,可得( )x2-8k1x=0,解得x=0或x=
)x2-8k1x=0,解得x=0或x= ,则点D的坐标为
,则点D的坐标为 ; …(14分)
; …(14分)
同理可得点E的坐标
于是S2= =
=
因此 ,…(16分)
,…(16分)
又由点A,B的坐标可知,k= =
= ,平方后代入上式,
,平方后代入上式,
所以λ=
故λ的取值范围为[ ). …(18分)
). …(18分)
点评:本题考查椭圆的标准方程,考查直线与抛物线、椭圆的位置关系,考查三角形面积的计算,属于中档题.
(2)①设直线的方程与抛物线方程联立,利用点M的坐标为(0,-1),可得kMAkMB=-1,从而得证;
②设直线的斜率为k1,则直线的方程为y=k1x-1,代入抛物线方程可得x2=k1x,从而可得点A的坐标、点B的坐标,进而可得S1,同理可得S2,进而可得比值,由此可得λ的取值范围.
解答:(1)解:由题意知:半长轴为2,则有2
 =2 …(3分)
=2 …(3分)∴b=1 …(4分)
(2)①证明:由题意知,直线l的斜率存在,设为k,则直线的方程为y=kx.
与抛物线方程联立,消去y可得x2-kx-1=0,…(6分)
设A(x1,y1),B(x2,y2),则x1,x2是上述方程的两个实根,于是x1+x2=k,x1x2=-1.…(7分)
又点M的坐标为(0,-1),所以kMAkMB=
 ×
× =
= =-1…(9分)
=-1…(9分)故MA⊥MB,即MD⊥ME,故
 …(10分)
…(10分)②设直线的斜率为k1,则直线的方程为y=k1x-1,代入抛物线方程可得x2=k1x,解得x=0或x=k1,则点A的坐标为(k1,
 ) …(12分)
) …(12分)同理可得点B的坐标为
 .
.于是
 =
= =
=
直线的方程为y=k1x-1,代入椭圆方程,消去y,可得(
 )x2-8k1x=0,解得x=0或x=
)x2-8k1x=0,解得x=0或x= ,则点D的坐标为
,则点D的坐标为 ; …(14分)
; …(14分)同理可得点E的坐标

于是S2=
 =
=
因此
 ,…(16分)
,…(16分)又由点A,B的坐标可知,k=
 =
= ,平方后代入上式,
,平方后代入上式,所以λ=

故λ的取值范围为[
 ). …(18分)
). …(18分)点评:本题考查椭圆的标准方程,考查直线与抛物线、椭圆的位置关系,考查三角形面积的计算,属于中档题.

练习册系列答案
相关题目
 如图,椭圆C1:
如图,椭圆C1: (2013•宁波模拟)如图,椭圆
(2013•宁波模拟)如图,椭圆 (2012•杨浦区二模)如图,椭圆C1:
(2012•杨浦区二模)如图,椭圆C1: (2012•临沂二模)如图,椭圆C1:
(2012•临沂二模)如图,椭圆C1: