��Ŀ����
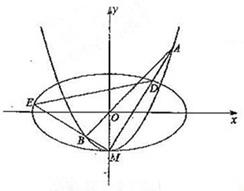 ��ͼ����ԲC1��
��ͼ����ԲC1��| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
������C1��C2�ķ��̣�
������C2��y��Ľ���ΪM��������ԭ��O��ֱ��l��C2�ཻ�ڵ�A��B��ֱ��MA��MB�ֱ���C1�ཻ��D��E��
��i��֤����MD��ME��
��ii���ǡ�MAB����MDE������ֱ���S1��S2���ʣ��Ƿ����ֱ��l��ʹ��
| S1 |
| S2 |
| 17 |
| 32 |
���������������������ʵõ�һ�����ڲ����ķ��̣�������x�ᱻ����C2��y=x2-b�صõ��߶γ�����C1�ij����᳤����һ�����̣�������������������������������C1��C2�ķ��̣�
����i����ֱ��l�ķ����������߷��������ɵù��ڵ�A��B����ĵ�����ϵ���ٴ������kMA•kMB=-1������֤����MD��ME��
��ii���Ȱ�ֱ��MA�ķ����������߷��������ɵõ�A�����꣬�������ҳ���ʽ���|MA|��ͬ���ķ������|MB|�������S1��ͬ������S2���ٴ�����֪�Ϳ�֪���Ƿ����ֱ��l�������������ˣ�
����i����ֱ��l�ķ����������߷��������ɵù��ڵ�A��B����ĵ�����ϵ���ٴ������kMA•kMB=-1������֤����MD��ME��
��ii���Ȱ�ֱ��MA�ķ����������߷��������ɵõ�A�����꣬�������ҳ���ʽ���|MA|��ͬ���ķ������|MB|�������S1��ͬ������S2���ٴ�����֪�Ϳ�֪���Ƿ����ֱ��l�������������ˣ�
����⣺���������e=
=
���Ӷ�a=2b����2
=a�����a=2��b=1��
��C1��C2�ķ��̷ֱ�Ϊ
+y2=1��y=x2-1��
����i������ã�ֱ��l��б�ʴ��ڣ���Ϊk����ֱ��l�ķ���Ϊy=kx��
��
��x2-kx-1=0��
��A��x1��y1����B��x2��y2������x1��x2���������̵�����ʵ����
����x1+x2=k��x1x2=-1���ֵ�M������Ϊ��0��-1����
����kMA•kMB=
•
=
=
=
=-1��
��MA��MB����MD��ME��
��ii����ֱ��MA��б��Ϊk1����ֱ��MA�ķ���Ϊy=k1x-1��
��
�����
��
��
���A��������k1��k12-1����
��ֱ��MB��б��Ϊ-
��ͬ���ɵõ�B������Ϊ��-
��
-1����
����s1=
|MA|•|MB|=
•|k1|•
•|-
|=
��
��
�ã�1+4k12��x2-8k1x=0��
���
��
�����D��������
��
����
��ֱ��ME��б��Ϊ-
��ͬ���ɵõ�E������Ϊ��
��
����
����s2=
|MD|•|ME|=
��
��
=
(4k12+
+17)=
�����k12=4��k12=
��
���ɵ�A��B������ã�k=
=k1-
������k=��
��
������������ֱ�ߴ��ڣ������������䷽��Ϊy=
x��y=-
x��
| c |
| a |
| ||
| 2 |
| b |
��C1��C2�ķ��̷ֱ�Ϊ
| x2 |
| 4 |
����i������ã�ֱ��l��б�ʴ��ڣ���Ϊk����ֱ��l�ķ���Ϊy=kx��
��
|
��A��x1��y1����B��x2��y2������x1��x2���������̵�����ʵ����
����x1+x2=k��x1x2=-1���ֵ�M������Ϊ��0��-1����
����kMA•kMB=
| y1+1 |
| x1 |
| y2+1 |
| x2 |
| (kx1+1)(kx2+1) |
| x1x2 |
| k2x1x2+k(x1+x2)+1 |
| x1x2 |
| -k2+k2+1 |
| -1 |
��MA��MB����MD��ME��
��ii����ֱ��MA��б��Ϊk1����ֱ��MA�ķ���Ϊy=k1x-1��
��
|
|
|
���A��������k1��k12-1����
��ֱ��MB��б��Ϊ-
| 1 |
| k1 |
| 1 |
| k1 |
| 1 |
| k12 |
����s1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1+k12 |
1+
|
| 1 |
| k1 |
| 1+k12 |
| 2|k1| |
��
|
���
|
|
| 8k1 |
| 1+4k12 |
| 4k12-1 |
| 1+4k12 |
��ֱ��ME��б��Ϊ-
| 1 |
| k1 |
| -8k1 |
| 4+k12 |
| 4-k12 |
| 4+k12 |
����s2=
| 1 |
| 2 |
| 32(1+k12)•|k1| |
| (1+4k12)(k12+4) |
��
| s1 |
| s2 |
| 1 |
| 64 |
| 4 |
| k12 |
| 17 |
| 32 |
| 1 |
| 4 |
���ɵ�A��B������ã�k=
k12-
| ||
k1+
|
| 1 |
| k1 |
| 3 |
| 2 |
������������ֱ�ߴ��ڣ������������䷽��Ϊy=
| 3 |
| 2 |
| 3 |
| 2 |
�����������Ƕ���Բ���������Լ�ֱ���������ߺ�ֱ������Բ���ۺ�����Ŀ��飮��һ���������̺��鷳���⣬��ҪҪ���棬ϸ�µ�̬�Ȳ��ܰ���Ŀ���ã�

��ϰ��ϵ�д�
 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д� �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�
�����Ŀ
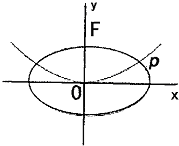 ��ͼ��������C1��x2=2py��p��0���Ľ���ΪF����ԲC2��
��ͼ��������C1��x2=2py��p��0���Ľ���ΪF����ԲC2�� ��2012•��������ģ����ͼ����ԲC1��
��2012•��������ģ����ͼ����ԲC1�� ��ͼ��������
��ͼ�������� ��ͼ����ԲC1��
��ͼ����ԲC1��