题目内容
【题目】p:关于x的方程![]() 无解,q:
无解,q:![]() (
(![]() )
)
(1)若![]() 时,“
时,“![]() ”为真命题,“
”为真命题,“![]() ”为假命题,求实数a的取值范围.
”为假命题,求实数a的取值范围.
(2)当命题“若p,则q”为真命题,“若q,则p”为假命题时,求实数m的取值范围.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() .
.
【解析】
(1)直接利用函数的性质和真值表的应用求出参数的取值范围.
(2)直接利用四个条件的应用和集合间的关系的应用求出结果.
(1)命题p:关于x的方程![]() 无解,
无解,
则:![]() ,
,
解得:![]() .
.
命题:q:![]() (
(![]() )
)
由于![]() ,
,
故:![]() .
.
由于“![]() ”为真命题,“
”为真命题,“![]() ”为假命题,
”为假命题,
故:①p真q假②p假q真,
故:①![]() ,无解.
,无解.
②
解得:![]() 或
或![]() ,
,
故:a的取值范围是:![]() 或
或![]() .
.
(2)命题“若p,则q”为真命题,“若q,则p”为假命题时,
故命题p为命题q的充分不必要条件.
故:命题p表示的集合![]() 是命题q表示的集合
是命题q表示的集合![]() 的真子集.
的真子集.
故:![]() ,
,
解得:![]() ,
,
当![]() 时:
时:![]() ,
,
故:![]() .
.

【题目】《朗读者》是一档文化情感类节目,以个人成长、情感体验、背景故事与传世佳作相结合的方式,选用精美的文字,用最平实的情感读出文字背后的价值,深受人们的喜爱.为了了解人们对该节目的喜爱程度,某调查机构随机调查了![]() ,
,![]() 两个城市各100名观众,得到下面的列联表.
两个城市各100名观众,得到下面的列联表.
非常喜爱 | 喜爱 | 合计 | |
| 60 | 100 | |
| 30 | ||
合计 | 200 |
完成上表,并根据以上数据,判断是否有![]() 的把握认为观众的喜爱程度与所处的城市有关?
的把握认为观众的喜爱程度与所处的城市有关?
附参考公式和数据: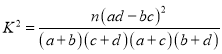 (其中
(其中![]() ).
).
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【题目】已知某观光海域AB段的长度为3百公里,一超级快艇在AB段航行,经过多次试验得到其每小时航行费用Q(单位:万元)与速度v(单位:百公里/小时)(0≤v≤3)的以下数据:
| 0 | 1 | 2 | 3 |
| 0 | 0.7 | 1.6 | 3.3 |
为描述该超级快艇每小时航行费用Q与速度v的关系,现有以下三种函数模型供选择:Q=av3+bv2+cv,Q=0.5v+a,Q=klogav+b.
(1)试从中确定最符合实际的函数模型,并求出相应的函数解析式;
(2)该超级快艇应以多大速度航行才能使AB段的航行费用最少?并求出最少航行费用.