题目内容
已知命题p1：函数y＝2x－2－x在R上为增函数，p2：函数y＝2x＋2－x在R上为减函数，则在命题q1：p1∨p2，q2：p1∧p2，q3：(¬p1)∨p2和q4：p1∧(¬p2)中，真命题是
| A．q1，q3 |
| B．q2，q3 |
| C．q1，q4 |
| D．q2，q4 |
C
解析∵2x在R上增函数,2-x在R上减函数,
∴y＝2x－2-x在R上为增函数,即p1为真命题, ¬p1为假命题
又∵y′=ln2(2x-2-x),当x>0时y′>0,即y＝2x+2-x为增函数;
当x<0时y′<0, 即y＝2x+2-x为减函数,即p2为假命题, ¬p2为真命题
所以q1为真，q2为假，q3为假，q4为真．
故选C
练习册系列答案
相关题目
下列命题中是假命题的是( )
A． 上递减 |
B． |
C． |
D． 都不是偶函数 |
“函数y=sin(x＋φ)为偶函数”是“φ＝
”的
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |
命题“对任意
，都有
”的否定是（ ）
A．存在 ，使得 | B．不存在，使得 |
C．存在，使得 | D．对任意，都有 |
已知
和
是指数函数，则“
”是“
”的( )
| A．充分不必要条件 | B．必要不充分条件 |
| C．充分必要条件 | D．既不充分也不必要条件 |
若向量
=（x，3）（x∈R），则“x=4”是“||=5”的（ ）
| A．充分而不必要条件 | B．必要而不充分条件 |
| C．充要条件 | D．既不充分又不必要条件 |
下列有关命题的说法正确的是 （ ）
A．命题“若 ，则 ”的否命题为：“若，则 ” |
B．“若 ，则 ， 互为相反数”的逆命题为真命题 |
C．命题“ ，使得 ”的否定是：“ ，均有” |
D．命题“若 ，则 ”的逆否命题为真命题 |
已知命题p：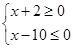
命题q：1－m≤x≤1＋m，m>0，若¬p是¬q的必要不充分
条件，则实数m的取值范围是( )
| A．m≥0 |
| B．m≥9 |
| C．m≤9 |
| D．m≤－2 |