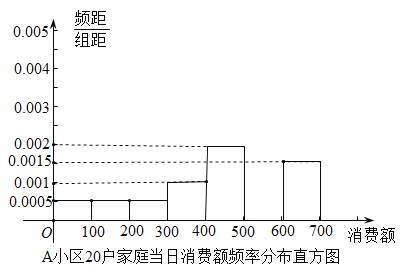
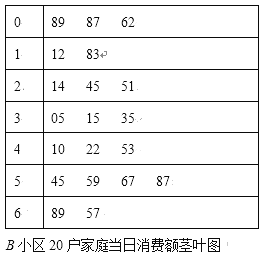
题目内容
【题目】已知椭圆
：
（
），点
是的左顶点，点
为上一点，离心率
.
（1）求椭圆的方程；
（2）设过点的直线
与的另一个交点为
（异于点
），是否存在直线，使得以
为直径的圆经过点，若存在，求出直线的方程；若不存在，说明理由.
【答案】（1）
；（2）存在，
【解析】
（1）把点
代入椭圆C的方程，再结合离心率，可得a,b,c的关系，可得椭圆的方程；
（2）设出直线
的方程，代入椭圆，运用韦达定理可求得点
的坐标，再由
，可求得直线的方程,要注意检验直线是否和椭圆有两个交点．
（1）由题可得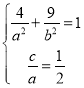
∴
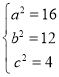，所以椭圆
的方程
（2）由题知
，设
，直线的斜率存在设为
，
则
与椭圆联立得
，
，∴
，
，∴
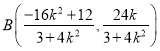
若以
为直径的圆经过点
，
则，∴
，
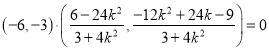化简得
，∴
，解得
或
因为与不重合，所以舍.
所以直线的方程为.
练习册系列答案
相关题目
【题目】已知函数
的定义域为
，部分对应值如下表：
|
| 0 | 4 | 5 |
| 1 | 2 | 2 | 1 |
的导函数
的图象如图所示，关于的命题正确的是（ ）
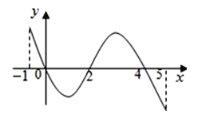
A.函数是周期函数
B.函数在
上是减函数
C.函数
的零点个数可能为0，1，2，3，4
D.当
时，函数有 4个零点
