题目内容
20．已知函数f（x）=$\left\{\begin{array}{l}{3-x，x≥1}\\{2x+1，x＜1}\end{array}\right.$，求$\underset{lim}{x→{1}^{-}}$f（x），$\underset{lim}{x→{1}^{+}}$f（x），并讨论函数f（x）在点x=1的极限是否存在？分析 根据函数解析式得出$\underset{lim}{x→{1}^{-}}$f（x），$\underset{lim}{x→{1}^{+}}$f（x），判断相等与否即可判断极限是否存在．
解答 解：∵函数f（x）=$\left\{\begin{array}{l}{3-x，x≥1}\\{2x+1，x＜1}\end{array}\right.$，
∴$\underset{lim}{x→{1}^{-}}$f（x）=2×1+1=3，$\underset{lim}{x→{1}^{+}}$f（x）=3-1=2，
∴$\underset{lim}{x→{1}^{-}}$f（x）≠$\underset{lim}{x→{1}^{+}}$f（x），
∴函数f（x）在点x=1的极限不存在
点评 本题简单的考察了极限的概念，极限的思想，关键利用左极限，右极限与在点的极限的关系．
练习册系列答案
相关题目
10．设x、y满足约束条件$\left\{\begin{array}{l}{x-2y+2≥0}\\{3x-2y-6≤0}\\{x≥0，y≥0}\end{array}\right.$若目标函数z=ax+by（a＞0，b＞0）的最大值为12，则a2+b2的最小值为（ ）
| A． | $\frac{25}{4}$ | B． | $\frac{49}{9}$ | C． | $\frac{144}{25}$ | D． | $\frac{225}{49}$ |
11．
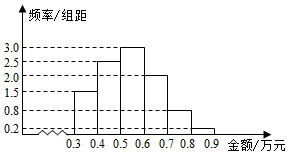某电子商务公司随机抽取l000名网络购物者进行调查，这1000名购物者2015年网上购物金额（单位：万元）均在区间[0.3，0.9]内，样本分组为：[0.3，0.4），[0.4，0.5），
[0.5，0.6），[0.6，0.7），[0.7，0.8），[0.8，0.9]，购物金额的频率分布直方图如下：电子商务公司决定给购物者发放优惠券，其金额（单位：元）与购物金额关系如下：
（I）求这1000名购物者获得优惠券金额的平均数；
（Ⅱ）以这1000名购物者购物金额落在相应区间的频率作为概率，求一个购物者获得优惠券金额不少于150元的概率．
某电子商务公司随机抽取l000名网络购物者进行调查，这1000名购物者2015年网上购物金额（单位：万元）均在区间[0.3，0.9]内，样本分组为：[0.3，0.4），[0.4，0.5），[0.5，0.6），[0.6，0.7），[0.7，0.8），[0.8，0.9]，购物金额的频率分布直方图如下：电子商务公司决定给购物者发放优惠券，其金额（单位：元）与购物金额关系如下：
| 购物金额分组 | [0.3，0.5） | [0.5，0.6） | [0.6，0.8） | [0.8，0.9] |
| 发放金额 | 50 | 100 | 150 | 200 |
（Ⅱ）以这1000名购物者购物金额落在相应区间的频率作为概率，求一个购物者获得优惠券金额不少于150元的概率．
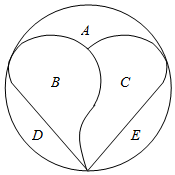如图所示，积木拼盘由A、B、C、D、E五块积木组成，若每块积木都要涂一种颜色，且为了体现拼盘的特色，相邻的区域需涂不同的颜色（如：A与B为相邻区域，A与D为不相邻区域），现有五种不同的颜色可供挑选，则可组成的不同的积木拼盘的种数是（ ）