题目内容
.如图,在底面是直角梯形的四棱锥 P—ABCD中,AD//BC, ∠ABC=90°,PA⊥平面ABCD,PA=4.
AD=2,AB= ,BC=6.
,BC=6.

(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)求二面角A—PC—D的余弦值.
【答案】
解法一:(1)∵PA⊥平面ABCD, BD 平面ABCD, ∴BD⊥PA.
平面ABCD, ∴BD⊥PA.
又
 ,
,
∴∠ABD=30,°∠BAC=60°
∴∠AEB=90°,即BD⊥AC ……4分
又PA AC=A, ∴BD⊥平面PAC.
AC=A, ∴BD⊥平面PAC.
(2)过E作EF⊥PC,垂足为F,连结DF,
∵DE⊥平面PAC,EF是DF在平面PAC上的射影,由三垂线定理知PC⊥DF,
∴∠EFD为二面角A—PC—D的平面角.
 又∠DAC=90°—∠BAC=30°∴DE=ADsin∠DAC=1,AE=ABsin∠ABE=
又∠DAC=90°—∠BAC=30°∴DE=ADsin∠DAC=1,AE=ABsin∠ABE= ,
,
又AC= ,
∴EC=
,
∴EC= , PC=8.
, PC=8.
由Rt△EFC∽Rt△PAC得
在Rt△EFD中, ,
,
∴ .∴二面角A—PC—D的大小为
.∴二面角A—PC—D的大小为 .
.
解法二:(1)如图,建立坐标系,则
 ……2分
……2分
∴ ,
, ∴
∴ ,
,
 ∴BD⊥AP, BD⊥AC, 又PA
∴BD⊥AP, BD⊥AC, 又PA AC=A∴BD⊥平面PAC.
AC=A∴BD⊥平面PAC.
(2)设平面PCD的法向量为 ,
,
则 , ……6分
, ……6分
又 ,
,
∴ , 解得
, 解得
∴ ……8分
……8分
平面PAC的法向量取为 , ……10分
, ……10分
 ∴二面角A—PC—D的大小为
∴二面角A—PC—D的大小为 .
.
【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
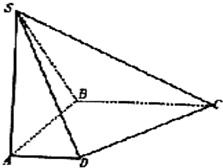 如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,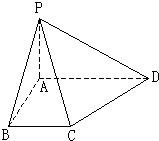 如图,在底面是直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,且
如图,在底面是直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,且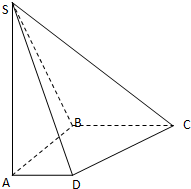 如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=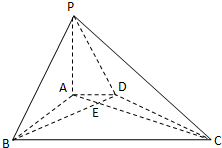 如图,在底面是直角梯形的四棱锥 P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=4.AD=2,AB=
如图,在底面是直角梯形的四棱锥 P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=4.AD=2,AB= 如图,在底面是直角梯形的四棱锥S-ABCD中,已知∠ABC=90°,SA⊥平面ABCD,AB=BC=2,AD=1.
如图,在底面是直角梯形的四棱锥S-ABCD中,已知∠ABC=90°,SA⊥平面ABCD,AB=BC=2,AD=1.