题目内容
(满分12分)
已知 是实数,函数
是实数,函数 .
.
(Ⅰ)若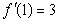 ,求
,求 的值及曲线
的值及曲线 在点
在点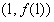 处的切线方程;
处的切线方程;
(Ⅱ)求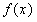 在区间
在区间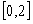 上的最大值.
上的最大值.
【答案】
(Ⅰ)可得曲线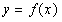 在
在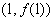 处的切线方程为
处的切线方程为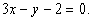
(Ⅱ)
【解析】(Ⅰ)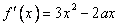 ,由
,由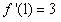 易得a=0,从而可得曲线
易得a=0,从而可得曲线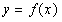 在
在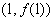 处的切线方程为
处的切线方程为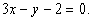 …………………………………………………………4分
…………………………………………………………4分
(Ⅱ)先求出可能的极值点x1=0,x2=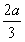 ,再讨论极值点与区间[0,2]端点的位置关系.令
,再讨论极值点与区间[0,2]端点的位置关系.令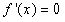 ,得
,得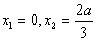 .
.
当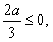 即
即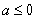 时,
时,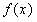 在
在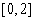 上单调递增,
上单调递增, 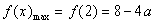 ;…6分
;…6分
当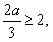 即
即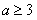 时,
时,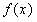 在
在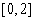 上单调递减,
上单调递减, 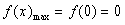 ;……8分
;……8分
当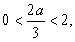 即
即 时,
时,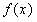 在
在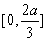 上单调递减,在
上单调递减,在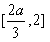 上单调递增,函数f(x)(0≤ x ≤2)的最大值只可能在x=0或x=2处取到,因为f(0)
=0,f(2)=8-4a,令f(2)
≥ f(0),得a ≤ 2,所以
上单调递增,函数f(x)(0≤ x ≤2)的最大值只可能在x=0或x=2处取到,因为f(0)
=0,f(2)=8-4a,令f(2)
≥ f(0),得a ≤ 2,所以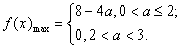 …………11分
…………11分
综上, ……………………………………………………12分
……………………………………………………12分

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
 bc.
bc. (常数
(常数 ),P是曲线C上的动点,M是曲线C的右
),P是曲线C上的动点,M是曲线C的右 ,求|PA|的最大值与最小值.
,求|PA|的最大值与最小值. 的取值范围.
的取值范围. ,
,
 时,
时, 在其定义域内单调递增,求
在其定义域内单调递增,求 的取值范围;
的取值范围; 的图象
的图象 与函数
与函数 的图象
的图象 交于
交于 ,
, 两点,过线段
两点,过线段 的中点
的中点 作
作 轴的垂线分别交
轴的垂线分别交 ,
, ,问是否存在点
,问是否存在点