题目内容
14.在△ABC中,$AB=3,AC=\sqrt{3},B=\frac{π}{6}$,则△ABC的面积等于( )| A. | $\frac{{3\sqrt{3}}}{2}$ | B. | $\frac{{3\sqrt{3}}}{4}$ | C. | $\frac{{3\sqrt{3}}}{2}$或$3\sqrt{3}$ | D. | $\frac{{3\sqrt{3}}}{2}$或$\frac{{3\sqrt{3}}}{4}$ |
分析 由已知利用正弦定理可求sinC,结合C的范围可求C,从而可求A,sinA的值,利用三角形面积公式即可得解.
解答 解:∵$AB=3,AC=\sqrt{3},B=\frac{π}{6}$,
∴由正弦定理可得:sinC=$\frac{ABsinB}{AC}$=$\frac{3×\frac{1}{2}}{\sqrt{3}}$=$\frac{\sqrt{3}}{2}$,
∴结合0<C<π,解得:C=$\frac{π}{3}$或$\frac{2π}{3}$,则A=π-B-C=$\frac{π}{2}$或$\frac{π}{6}$,可求得:sinA=1或$\frac{1}{2}$
∴S△ABC=$\frac{1}{2}$AC•AB•sinA=$\frac{1}{2}×\sqrt{3}×3×$sinA=$\frac{3\sqrt{3}}{2}$或$\frac{3\sqrt{3}}{4}$.
故选:D.
点评 本题主要考查了正弦定理,三角形面积公式,三角形内角和定理,特殊角的三角函数值的综合应用,属于基本知识的考查.

练习册系列答案
相关题目
8.函数f(x)=Asin(wx+φ)(A>0,w>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{3π}{2}$)的值是( )
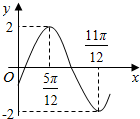

| A. | -1 | B. | 1 | C. | -$\sqrt{3}$ | D. | $\sqrt{3}$ |
5.已知向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(2,m2),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则 m的值为( )
| A. | 2或-1 | B. | -2或1 | C. | ±2 | D. | ±1 |
19.设全集I=R,若集合M={y|y=2${\;}^{\sqrt{3+2x-{x}^{2}}}$},N={x|y=ln(x-2)},则M∩∁I(N)=( )
| A. | [2,4] | B. | [1,2] | C. | (-∞,2]∪[4,+∞) | D. | (-∞,1]∪[2,+∞) |
6.f(x)为奇函数,且在(-∞,0)为递增,f(-2)=0,则xf(x)>0的解集为( )
| A. | (-∞,-2)∪(2,+∞) | B. | (-∞,-2)∪(0,2) | C. | (-2,0)∪(0,2) | D. | (-2,0)∪(2,+∞) |
3.有下列四个命题:
(1)“若xy>0,则x,y同正、或同负”的逆命题
(2)“周长相等的两个三角形全等”的否命题
(3)“若m≤1,则x2-2x+m=0有实数解”的逆否命题
(4)“若A∩B=B,则A⊆B”的逆否命题
其中真命题为( )
(1)“若xy>0,则x,y同正、或同负”的逆命题
(2)“周长相等的两个三角形全等”的否命题
(3)“若m≤1,则x2-2x+m=0有实数解”的逆否命题
(4)“若A∩B=B,则A⊆B”的逆否命题
其中真命题为( )
| A. | (1)(2) | B. | (2)(3) | C. | (3)(4) | D. | (1)(2)(3) |
4.已知a>0,b>0,a+b=200,则lga+lgb的最大值为( )
| A. | 1 | B. | 2 | C. | 4 | D. | 10 |