Question

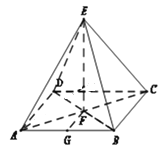
【题目】如图所示，是正方形所在平面外一点，在面上的投影为，，，，有以下四个命题：

（1）面；

（2）为中点，且；

（3）以，作为邻边的平行四边形面积是32；

（4）的内切球半径为.

其中正确命题的个数为（ ）

A.1B.2C.3D.4

Answer 1

【答案】C

【解析】

(1)先证,再根据直线与平面垂直的判定定理可证结论正确;

(2)通过证明,可得垂直平分,同理可得点在线段的垂直平分线上,从而可得为正方形的中心,在中可求得,可知(2)正确;

(3)利用平行四边形的面积公式求得面积为16,所以(3)错误;

(4)利用可求得内切球的半径为,所以(4)错误.

解：(1)如图，连接，

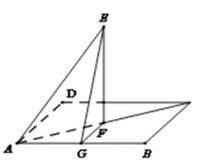
∵在平面上的投影为，∴面，

又∵面，∴，

∵为正方形，∴，

∵，∴.

又∵，，∴面，

所以（1）正确;

(2)连接、,

∵，，∴为正三角形，∴,

∵面，面，面，

∴，，即，

又∵，

∴，∴，

∴点在线段的垂直平分线上，

∵，，

∴，∴垂直平分.

同理可证点在线段的垂直平分线上，

∴为正方形的中心，

∵，∴，

又∵，，

∴中，，

∴，

所以(2)正确.;

(3)由(2)知，

以、作为邻边的平行四边形的面积为，

所以，(3)错误.

(4)∵为正方形，在底面的投影为正方形的中心，

∴为正四棱锥,

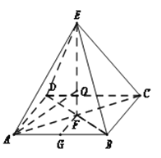
设正四棱锥内切球球心为，半径为，如图所示:

则：

，

又∵.

，

，

∴，

∴.

所以(4)正确.

故选:C