Question

【题目】已知F为抛物线的焦点，F关于原点的对称点为，点M在抛物线C上，给出下列三个结论：

①使得为等腰三角形的点M有且仅有6个

②使得的点M有且仅有2个

③使得的点M有且仅有4个

其中正确结论的个数为（ ）

A.0B.1C.2D.3

Answer 1

【答案】A

【解析】

根据抛物线的性质对四个选项分别判断．

为等腰三角形，若，这样的点有两个，若，这样的点有两个，满足的点有一个但不能构成三角形．故点只有4个，①错；

由，而，，所以满足的点不存在，②错；

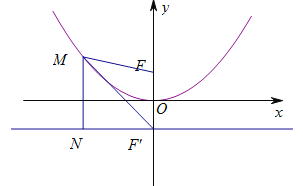
如图，作垂直于抛物线的准线（准线显然过点），垂足为，则，若则，所以，

又，设直线的倾斜角为，其方程为，代入抛物线方程整理得：，，此方程是两个相等实根，即直线与抛物线只有一个公共点，根据对称性，满足的点有两个，③错．

故选：A．