Question

（14分）已知函数f(x)=在x=-2处有极值.

（Ⅰ）求函数f(x)的单调区间；

（Ⅱ）若函数f(x)在区间[-3,3]上有且仅有一个零点，求b的取值范围.

Answer 1

（14分）

解: （Ⅰ）       …………………………………………1分

由题意知: ,得a=-1，………………………2分

∴，

令，得x<-2或x>0,           ………………………4分

 令，得-2<x<0,              ………………………5分

∴f(x)的单调递增区间是（-¥，-2）和（0，+¥），

单调递减区间是（-2，0）。…………………………………………6分

（Ⅱ）由（Ⅰ）知，f(x)= ，

f(-2)=为函数f(x)极大值，f(0)=b为极小值。…………………8分

∵函数f(x)在区间[-3,3]上有且仅有一个零点，

∴或或或或  ，

即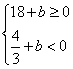  ，…………………………………………………………13分

∴，即b的取值范围是。  …………………14分