题目内容
当圆 的面积最大时,圆心坐标是 ( )
的面积最大时,圆心坐标是 ( )
A. | B. | C. | D. |
B
解析试题分析:根据已知中圆 通过配方法,得到圆的标准方程
通过配方法,得到圆的标准方程
圆 ,那么可知圆心坐标为(-1,-
,那么可知圆心坐标为(-1,- ),半径的平方为
),半径的平方为 ,那么要是圆的面积最大,那么则使得
,那么要是圆的面积最大,那么则使得 最大,
最大, ,可知圆的半径的最大值为1,那么可知此时k=0,那么圆心的坐标为(-1,0),故选B.
,可知圆的半径的最大值为1,那么可知此时k=0,那么圆心的坐标为(-1,0),故选B.
考点:本试题主要是考查了圆的面积问题的最值运用。
点评:解决圆的面积的最大值,就是求解圆的半径的最大值即可。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若直线 始终平分圆
始终平分圆 的周长,则
的周长,则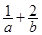 的最小值为
的最小值为
| A.1 | B.5 | C.3+ | D. |
点 与圆
与圆 上任一点连线的中点轨迹方程是( )
上任一点连线的中点轨迹方程是( )
A. | B. |
C. | D. |
直线 与圆
与圆 相切,则
相切,则 的值为 ( )
的值为 ( )
A. | B. | C.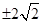 | D. |
由直线 上的一点向圆
上的一点向圆 引切线,则切线长的最小值为( )
引切线,则切线长的最小值为( )
| A.1 | B. | C.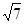 | D.3 |
已知直线 与圆
与圆 交于
交于 两点,且
两点,且 ,则实数
,则实数 的值为( )
的值为( )
| A.2 | B.-2 | C.2或-2 | D. 或 或 |
设P(x,y)是曲线C: 上任意一点,则
上任意一点,则 的取值范围是
的取值范围是
A. | B. |
C. | D. |
 上至少有三个不同的点到直线
上至少有三个不同的点到直线 的
的 则直线
则直线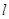 的倾斜角的取值范围是( )
的倾斜角的取值范围是( )







 轴上,半径为1,且过点
轴上,半径为1,且过点  的圆的方程 ( )
的圆的方程 ( ) B
B 
 D
D 