题目内容
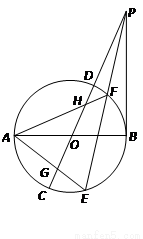
如图,设AB,CD为⊙O的两直径,过B作PB垂直于AB,并与CD延长线相交于点P,过P作直线与⊙O分别交于E,F两点,连结AE,AF分别与CD交于G、H

(Ⅰ)设EF中点为 ,求证:O、
,求证:O、 、B、P四点共圆
、B、P四点共圆
(Ⅱ)求证:OG =OH.
【答案】
(Ⅰ)由 ,推出
,推出 四点共圆.
四点共圆.
(Ⅱ)先证得 四点共圆. 在得出
四点共圆. 在得出 ∥
∥ ,由
,由 是
是 的中点,
的中点, 是
是 的中点,推出
的中点,推出 ,得到OG =OH。
,得到OG =OH。
【解析】
试题分析:(Ⅰ)
易知 ,
,
所以 四点共圆. 3分
四点共圆. 3分
(Ⅱ)由(Ⅰ)
过 作
作 于
于 ,交
,交 于
于
连结
由 ∥
∥ ,
, 
所以

所以 四点共圆.
6分
四点共圆.
6分
所以 ,由此
,由此 ∥
∥ , 8分
, 8分
 是
是 的中点,
的中点, 是
是 的中点,所以
的中点,所以 ,所以OG ="OH" 10分
,所以OG ="OH" 10分

考点:本题主要考查圆的性质,三角形相似。
点评:中档题,在研究平面几何问题时,适当添加“辅助线”,往往是解决问题的关键。

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
 ,求证:O、
,求证:O、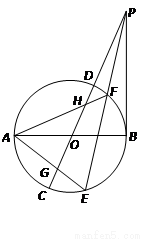
 ,求证:O、
,求证:O、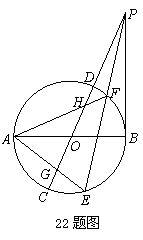 (Ⅰ)设EF中点为
(Ⅰ)设EF中点为