题目内容
设点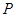 是双曲线
是双曲线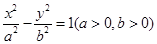 与圆
与圆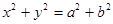 在第一象限的交点,其中
在第一象限的交点,其中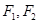 分别是双曲线的左、右焦点,若
分别是双曲线的左、右焦点,若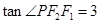 ,则双曲线的离心率为______________.
,则双曲线的离心率为______________.
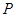 是双曲线
是双曲线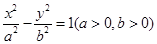 与圆
与圆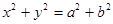 在第一象限的交点,其中
在第一象限的交点,其中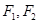 分别是双曲线的左、右焦点,若
分别是双曲线的左、右焦点,若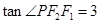 ,则双曲线的离心率为______________.
,则双曲线的离心率为______________.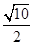
试题分析:先由双曲线定义和已知求出两个焦半径的长,再由已知圆的半径为半焦距,知焦点三角形为直角三角形,从而由勾股定理得关于a、c的等式,求得离心率解:依据双曲线的定义:|PF1|-|PF2|=2a,又∵
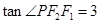 ,即|PF1|=3|PF2|,∴|PF1|=3a,|PF2|=a,∵圆x2+y2=a2+b2的半径r=c,∴F1F2是圆的直径,∴∠F1PF2=90°在直角三角形F1PF2中由(3a)2+a2=(2c)2,得e=
,即|PF1|=3|PF2|,∴|PF1|=3a,|PF2|=a,∵圆x2+y2=a2+b2的半径r=c,∴F1F2是圆的直径,∴∠F1PF2=90°在直角三角形F1PF2中由(3a)2+a2=(2c)2,得e=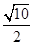 ,故填写
,故填写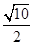
点评:本题考查了双曲线的定义,双曲线的几何性质,离心率的求法

练习册系列答案
相关题目
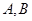 是椭圆
是椭圆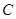 :
: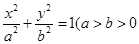 且
且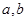 为常数
为常数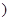 上关于原点对称的两点,点
上关于原点对称的两点,点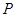 是椭圆上的任意一点,若直线
是椭圆上的任意一点,若直线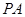 和
和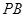 的斜率都存在,并分别记为
的斜率都存在,并分别记为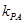 ,
,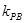 ,那么
,那么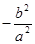 .
.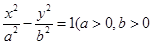 且
且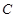 的左右焦点分别为
的左右焦点分别为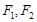 ,且
,且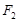 恰为抛物线
恰为抛物线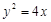 的焦点,设双曲线
的焦点,设双曲线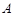 ,若
,若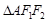 是以
是以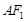 为底边的等腰直角三角形,则双曲线
为底边的等腰直角三角形,则双曲线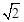
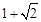
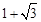
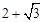
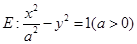 的离心率等于
的离心率等于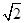 ,直线
,直线 与双曲线
与双曲线 的右支交于
的右支交于 两点.
两点.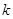 的取值范围;
的取值范围; ,点
,点 是双曲线
是双曲线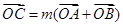 ,求
,求
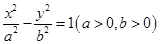 的两个焦点恰为椭圆
的两个焦点恰为椭圆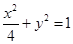 的两个顶点,且离心率为2,则该双曲线的标准方程为 ( )
的两个顶点,且离心率为2,则该双曲线的标准方程为 ( )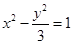
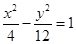
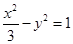
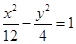
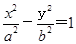 (a>0,b>0)的离心率是
(a>0,b>0)的离心率是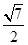 ,则
,则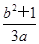 的最小值为 ( )
的最小值为 ( )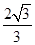
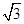
 -m
-m




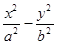 =1(a>0,b>0)的离心率为2,坐标原点到直线AB的距离为
=1(a>0,b>0)的离心率为2,坐标原点到直线AB的距离为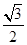 ,其中A(0,-b),B(a,0).
,其中A(0,-b),B(a,0).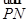 ·
·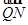 =0,且|
=0,且|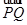 |=10,求直线l的方程.
|=10,求直线l的方程.