题目内容
设数列 满足
满足 ,
, ,且对任意
,且对任意 ,函数
,函数 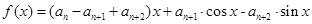 满足
满足
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若 ,求数列
,求数列 的前
的前 项和
项和 .
.
 满足
满足 ,
, ,且对任意
,且对任意 ,函数
,函数 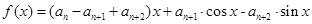 满足
满足
(Ⅰ)求数列
 的通项公式;
的通项公式;(Ⅱ)若
 ,求数列
,求数列 的前
的前 项和
项和 .
.(Ⅰ)  (Ⅱ)
(Ⅱ)
 (Ⅱ)
(Ⅱ)
由




所以,
 是等差数列.
是等差数列.
而



(2)


第(1)题,通过求导以及 ,能够判断出
,能够判断出 是等差数列是等差数列,由第(1)题的结论能够写出
是等差数列是等差数列,由第(1)题的结论能够写出 的通项公式,根据
的通项公式,根据 的特征,选择求和的方法,利用分组求和的方法即可求出.
的特征,选择求和的方法,利用分组求和的方法即可求出.
【考点定位】考查函数的求导法则和求导公式,等差、等比数列的性质和数列基本量的求解.并考查逻辑推理能力和运算能力.





所以,

 是等差数列.
是等差数列.而




(2)



第(1)题,通过求导以及
 ,能够判断出
,能够判断出 是等差数列是等差数列,由第(1)题的结论能够写出
是等差数列是等差数列,由第(1)题的结论能够写出 的通项公式,根据
的通项公式,根据 的特征,选择求和的方法,利用分组求和的方法即可求出.
的特征,选择求和的方法,利用分组求和的方法即可求出.【考点定位】考查函数的求导法则和求导公式,等差、等比数列的性质和数列基本量的求解.并考查逻辑推理能力和运算能力.

练习册系列答案
相关题目
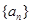 的前
的前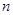 项和为
项和为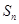 ,且满足
,且满足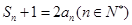 .
.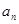 与
与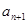 两项之间插入
两项之间插入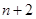 个数构成等差数列,其公差为
个数构成等差数列,其公差为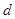 ,求数列
,求数列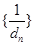 的前
的前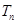 .
.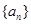 的通项公式为
的通项公式为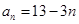 ,
,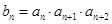 ,
,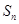 是数列
是数列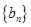 的前
的前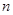 项和,则
项和,则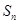 的最大值为( )
的最大值为( )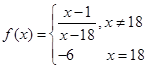 ,则
,则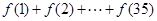 的值为 .
的值为 . 的前n项和
的前n项和 ,则( )
,则( ) 的前
的前 项和为
项和为 ,且
,且 …);
…); 满足
满足 …),
…), 求数列
求数列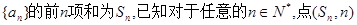 都在函数
都在函数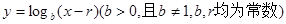 的图象上。
的图象上。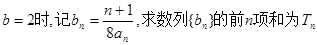 ;
;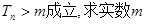 的取值范围。
的取值范围。 的前
的前 项和为
项和为 ,若点
,若点
 在函数
在函数 的图像上,则
的图像上,则



 共有
共有 项,其中奇数项通项公式为
项,其中奇数项通项公式为 ,则数列
,则数列


