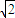题目内容
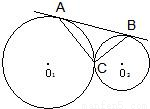
已知:如图,⊙O1与⊙O2外切于C点,AB一条外公切线,A、B分别为切点,连接AC、BC.设⊙O1的半径为R,⊙O2的半径为r,若tan∠ABC=
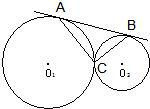
,则
的值为( )
| 2 |
| R |
| r |
A.
| B.
| C.2 | D.3 |

如图,连接O2B,O1A,过点C作两圆的公切线CF,交于AB于点F,作O1E⊥AC,O2D⊥BC,
由垂径定理可证得点E,点D分别是AC,BC的中点,
由弦切角定理知,

∠ABC=∠FCB=
∠BO2C,∠BAC=∠FCA=
∠AO1C,
∵AO1∥O2B,
∴∠AO1C+∠BO2C=180°,
∴∠FCB+∠FCA=∠ACB=90°,
即△ACB是直角三角形,
∴∠ABC=∠BO2D=∠ACO1,
设∠ABC=∠BO2D=∠ACO1=β,
则有sinβ=
,cosβ=
,
∴tanβ=
?
=
?
,
∴(tanβ)2=
=2.
故选C.
由垂径定理可证得点E,点D分别是AC,BC的中点,
由弦切角定理知,

∠ABC=∠FCB=
| 1 |
| 2 |
| 1 |
| 2 |
∵AO1∥O2B,
∴∠AO1C+∠BO2C=180°,
∴∠FCB+∠FCA=∠ACB=90°,
即△ACB是直角三角形,
∴∠ABC=∠BO2D=∠ACO1,
设∠ABC=∠BO2D=∠ACO1=β,
则有sinβ=
| BC |
| 2r |
| AC |
| 2R |
∴tanβ=
| R |
| r |
| BC |
| AC |
| R |
| r |
| 1 |
| tanβ |
∴(tanβ)2=
| R |
| r |
故选C.

练习册系列答案
相关题目
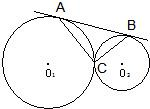 已知:如图,⊙O1与⊙O2外切于C点,AB一条外公切线,A、B分别为切点,连接AC、BC.设⊙O1的半径为R,⊙O2的半径为r,若tan∠ABC=
已知:如图,⊙O1与⊙O2外切于C点,AB一条外公切线,A、B分别为切点,连接AC、BC.设⊙O1的半径为R,⊙O2的半径为r,若tan∠ABC=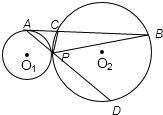

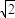 ,则
,则  的值为( )
的值为( )