题目内容
已知函数 ,(x∈R,a,b为实数)
,(x∈R,a,b为实数)
(Ⅰ)若x=1是函数f(x)的零点,求证:函数f(x)不是单调函数;
(Ⅱ)若函数f(x)在区间[-1,2]上是单调减函数,求a+b的最小值.
解:(I)∵f(1)= +a-b+1=0
+a-b+1=0
∴b=a+
∴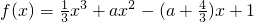
∴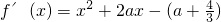
△=4a2+4(a+ )=4
)=4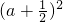 +
+ >0
>0
∴f′(x)=0必有两个不同的实根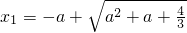 ,
,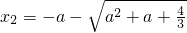 ,
,
当x∈(-∞,x1),f′(x)>0,
x∈(x1,x2),f′(x)<0,
x∈(x2,+∞),f′(x)>0,
故f(x)存在两个极值点即f(x)不是单调函数.
(II)∵函数f(x)在区间[-1,2]上是单调减函数
∴函数在[-1,2]上有f′(x)≤0恒成立
 即
即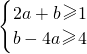
∵a+b= (2a+b)+
(2a+b)+ (b-4a)≥
(b-4a)≥ +
+ ×4=
×4=
∴a+b最小值为
分析:(I)根据x=1是函数f(x)的零点将b用a表示,然后研究函数的导数,求出f′(x)=0的根,然后判定函数的单调性即可;
(II)将函数f(x)在区间[-1,2]上是单调减函数转化成函数在[-1,2]上有f′(x)≤0恒成立,建立a、b的不等关系,然后利用a+b= (2a+b)+
(2a+b)+ (b-4a)可求出所求.
(b-4a)可求出所求.
点评:本题主要考查了利用导数研究函数的单调性,以及不等式的应用,同时考查了转化的数学思想和计算能力,属于中档题.
 +a-b+1=0
+a-b+1=0∴b=a+

∴
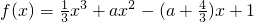
∴
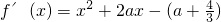
△=4a2+4(a+
 )=4
)=4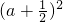 +
+ >0
>0∴f′(x)=0必有两个不同的实根
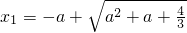 ,
,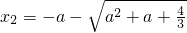 ,
,当x∈(-∞,x1),f′(x)>0,
x∈(x1,x2),f′(x)<0,
x∈(x2,+∞),f′(x)>0,
故f(x)存在两个极值点即f(x)不是单调函数.
(II)∵函数f(x)在区间[-1,2]上是单调减函数
∴函数在[-1,2]上有f′(x)≤0恒成立
 即
即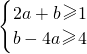
∵a+b=
 (2a+b)+
(2a+b)+ (b-4a)≥
(b-4a)≥ +
+ ×4=
×4=
∴a+b最小值为

分析:(I)根据x=1是函数f(x)的零点将b用a表示,然后研究函数的导数,求出f′(x)=0的根,然后判定函数的单调性即可;
(II)将函数f(x)在区间[-1,2]上是单调减函数转化成函数在[-1,2]上有f′(x)≤0恒成立,建立a、b的不等关系,然后利用a+b=
 (2a+b)+
(2a+b)+ (b-4a)可求出所求.
(b-4a)可求出所求.点评:本题主要考查了利用导数研究函数的单调性,以及不等式的应用,同时考查了转化的数学思想和计算能力,属于中档题.

练习册系列答案
相关题目
 (其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为
(其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为 ,且图象上一个点为
,且图象上一个点为 .
. 恒成立;q:函数y=(m2-1)x是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.
恒成立;q:函数y=(m2-1)x是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围. (其中x∈R,A>0,ω>0)的最大值为2,最小正周期为8.
(其中x∈R,A>0,ω>0)的最大值为2,最小正周期为8. ,其中x∈R,则下列结论中正确的是( )
,其中x∈R,则下列结论中正确的是( )
 的图象左移
的图象左移 得到函数f(x)的图象
得到函数f(x)的图象 (x∈R,且x≠1),那么它的反函数为( )
(x∈R,且x≠1),那么它的反函数为( ) (x∈R,且x≠1)
(x∈R,且x≠1) (x∈R,且x≠6)
(x∈R,且x≠6) (x∈R,且x≠-
(x∈R,且x≠- )
)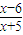 (x∈R,且x≠-5)
(x∈R,且x≠-5)