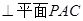题目内容
(本小题15分)
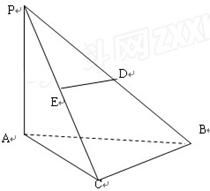
如图在三棱锥P-ABC中,PA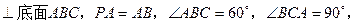
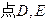 分别在棱
分别在棱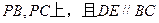 ,
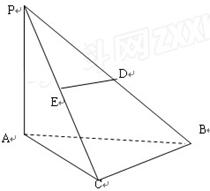
,
(1)求证:BC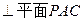
(2)当D为PB中点时,求AD与平面PAC所成的角的余弦值;
(3)是否存在点E,使得二面角A-DE-P为直二面角,并说明理由。

解:(1)


(2)建立空间直角坐标系如图,各点坐标分别为:
P(0,0,1),B(0,1,0), C

 ,
,
由DE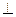 平面PAC可知,
平面PAC可知, 即是所求的二面角的平面角。
即是所求的二面角的平面角。 ,故所求二面角的余弦值为
,故所求二面角的余弦值为
(3)设D点的 轴坐标为a,
轴坐标为a,

 ,所以符合题意的E存在。
,所以符合题意的E存在。
解析

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
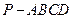 的底面
的底面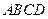 为一直角梯形,其中
为一直角梯形,其中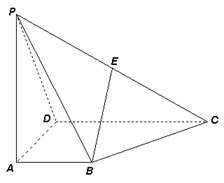
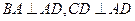 ,
,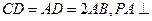 底面
底面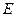 是
是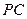 的中点.
的中点. //平面
//平面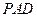 ;
;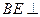 平面
平面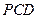 ,
,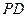 与
与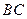 所成角的余弦值;
所成角的余弦值;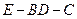 的余弦值.
的余弦值.
 .
.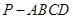 的底面
的底面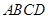 为一直角梯形,其中
为一直角梯形,其中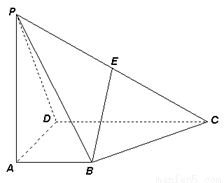
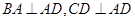 ,
,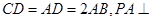 底面
底面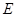 是
是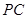 的中点.
的中点.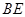 //平面
//平面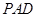 ;
; 平面
平面 ,
,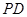 与
与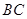 所成角的余弦值;
所成角的余弦值;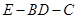 的余弦值.
的余弦值.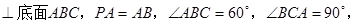
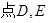 分别在棱
分别在棱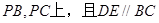 ,
,