题目内容
如图,要设计一张矩形广告,该广告含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为18000cm2,四周空白的宽度为10cm,两栏之间的中缝空白的宽度为5cm,怎样确定广告的高与宽的尺寸(单位:cm),能使矩形广告面积最小?

解:设矩形栏目的高为a cm,宽为b cm,则ab=9000, ①
广告的高为a+20,宽为2b+25,其中a>0,b>0,
广告的面积S=(a+20)(2b+25)
=2ab+40b+25a+500=18500+25a+40b
≥18500+2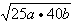 =18500+
=18500+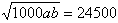 ,
,
当且仅当25a=40b时等号成立,
此时b=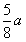 ,
,
代入①式得a=120,从而b=75,
即当a=120,b=75时,S取得最小值24500,
故广告的高为140 cm,宽为175 cm时,可使广告的面积最小。
广告的高为a+20,宽为2b+25,其中a>0,b>0,
广告的面积S=(a+20)(2b+25)
=2ab+40b+25a+500=18500+25a+40b
≥18500+2
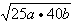 =18500+
=18500+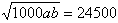 ,
,当且仅当25a=40b时等号成立,
此时b=
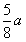 ,
,代入①式得a=120,从而b=75,
即当a=120,b=75时,S取得最小值24500,
故广告的高为140 cm,宽为175 cm时,可使广告的面积最小。

练习册系列答案
相关题目
 如图,要设计一张矩形广告,该广告含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为18000cm2,四周空白的宽度为10cm,两栏之间的中缝空白的宽度为5cm,怎样确定广告的高与宽的尺寸(单位:cm),能使矩形广告面积最小?
如图,要设计一张矩形广告,该广告含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为18000cm2,四周空白的宽度为10cm,两栏之间的中缝空白的宽度为5cm,怎样确定广告的高与宽的尺寸(单位:cm),能使矩形广告面积最小?


 四周空白的宽度为
四周空白的宽度为 ,两栏之间的中缝空白宽度为
,两栏之间的中缝空白宽度为 ,怎样确定广告的高与宽的尺寸(单位:cm),能使矩形广告面积最小?
,怎样确定广告的高与宽的尺寸(单位:cm),能使矩形广告面积最小?