题目内容
已知函数
（1）求函数f（x）的值域和最小正周期；
（2）当x∈[0，2π]时，求使
成立的x的值．
【答案】分析：（1）由已知中函数的解析式，及和差角公式，我们可将函数的解析式化简为正弦型函数的形式，求出A及ω值后，易得函数f（x）的值域和最小正周期；
（2）根据化简后的解析式，结合x∈[0，2π]，我们可求出使
成立的x的值．
解答：解：∵
=
=
=
=
=2sin（x+
）
（1）∵A=2，ω=1
∴ymax=2，ymin=2，T=2π
即函数f（x）的值域为[-2，2]和最小正周期为2π；
（2）若
则sin（x+
）=
又∵x∈[0，2π]
∴x+
∈[
，
]
则x+
∈{
，
，
}
则x={0，
，2π}
使
成立的x的值为0或
或2π
点评：本题考查的知识点是和差角公式，三角函数的周期，值域，三角函数给值求角，其中（2）中易忽略x=2π也满足条件．
（2）根据化简后的解析式，结合x∈[0，2π]，我们可求出使
成立的x的值．解答：解：∵
=
=
=
=
=2sin（x+
）（1）∵A=2，ω=1
∴ymax=2，ymin=2，T=2π
即函数f（x）的值域为[-2，2]和最小正周期为2π；
（2）若
则sin（x+
）=又∵x∈[0，2π]
∴x+
∈[，]则x+
∈{，，}则x={0，
，2π}使
成立的x的值为0或或2π点评：本题考查的知识点是和差角公式，三角函数的周期，值域，三角函数给值求角，其中（2）中易忽略x=2π也满足条件．
练习册系列答案
黄冈创优卷系列答案
相关题目
（1）求函数
在区间[1，
]上的最大值、最小值；
）上，函数
图象的下方；
，求证：
≥
。（
）
的极值点；
过点（0，—1），并且与曲线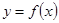
相切，求直线
，其中
，求函数
在
上的最小值.（其中e为自然对数的底数）