题目内容
(本小题共13分)已知函数 .
.
(Ⅰ)求函数 的极小值;
的极小值;
(Ⅱ)过点 能否存在曲线
能否存在曲线 的切线,请说明理由.
的切线,请说明理由.
0, 当 时存在切线;当
时存在切线;当 时不存在切线
时不存在切线
【解析】
试题分析:(Ⅰ)函数的定义域为R.
因为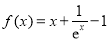 ,
,
所以 .
.
令 ,则
,则 .
.
|
| 0 |
|
| - | 0 | + |
| ↘ | 极小值 | ↗ |
所以 . 6分
. 6分
(Ⅱ)假设存在切线,设切点坐标为 ,
,
则切线方程为
即
将 代入得
代入得 .
.
方程 有解,等价于过点
有解,等价于过点 作曲线
作曲线 的切线存在.
的切线存在.
令 , 所以
, 所以 .
.
当 时,
时, .
.
所以 当 时,
时, ,函数
,函数 在
在 上单调递增;
上单调递增;
当 时,
时, ,
, 在
在 上单调递减.
上单调递减.
所以 当 时,
时, ,无最小值.
,无最小值.
当 时,方程
时,方程 有解;
有解;
当 时,方程
时,方程 无解.
无解.
综上所述,当 时存在切线;当
时存在切线;当 时不存在切线. 13分
时不存在切线. 13分
考点:本题考查导数的几何意义,用导数求极值

练习册系列答案
相关题目





 B.
B.
 D.
D.
 ,
, ,
, . 若
. 若 ,则实数
,则实数 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 的前n项和
的前n项和 则
则 = .
= . 若
若 ,则角B
,则角B B.
B.  C.
C. D.
D. 
 ,那么圆心坐标是 ;如果圆C的弦AB的中点坐标是(-2,3),那么弦AB所在的直线方程是___.
,那么圆心坐标是 ;如果圆C的弦AB的中点坐标是(-2,3),那么弦AB所在的直线方程是___.  (b>0且b≠1)的图象如图所示,那么函数
(b>0且b≠1)的图象如图所示,那么函数 的图象可能是
的图象可能是

 的离心率是 ;渐近线方程是 .
的离心率是 ;渐近线方程是 . ,则
,则 ( )
( ) B.
B. C.-
C.- D.
D.