Question

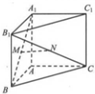如图，在直三棱柱ABC-A₁B₁C₁D₁中，点M是A₁B的中点，点N是B₁C的中点，连接MN．
（I）证明：MN∥平面ABC；
（II）若AB=1，AC=AA1═

3

，BC=2，点P是CC₁的中点，求四面体B₁-APB的体积．

Answer 1

分析：（1）连接AB₁，可证MN∥AC，利用线面平行的判定定理可证MN∥平面ABC；
（2）利用AB=1，AC=AA1═

3

，BC=2，可证明AB⊥AC，AA₁⊥AC，即AC⊥平面ABB₁A₁，从而VB1-APB=VP-B1AB=

1

3

•S△ABB1•AC，问题即可解决．

解答：证明：（Ⅰ）连接AB₁，
∵四边形A₁ABB₁是矩形，点M是A₁B的中点，
∴点M是AB₁的中点，
∵点N是B₁C的中点，
∴MN∥AC，
∵NM?平面ABC，AC?平面ABC，
∴MN∥平面ABC，…6
（Ⅱ）∵AB=1，AC=AA1═

3

，BC=2，
∴AB²+AC²=BC²，
∴AB⊥AC，
∵AA₁⊥AC，AA₁∩AB=A，
∴AC⊥平面ABB₁A₁，又CC₁∥平面ABB₁A₁，
∴P到平面平面ABB₁A₁的距离就是AC的长度．
∴VB1-APB=VP-B1AB=

1

3

S△ABB1•AC=

1

3

×

1

2

×1×

3

×

3

=

1

2

…12

点评：本题考查直线与平面垂直的判定，直线与平面平行的判定，着重考查两判定定理的应用，考查体积转化思想，属于中档题．