题目内容

设函数.

（1）求函数的单调递增区间；

（2）若函数的最小值为－1，求k的值并求此时x的取值集合

（1）（以上）（2）k=0  


解析:

（1）函数

＝                             ┉┉2分

 

，＝＝                     ┉┉4分

由,得函数的单调递增区

间是（以上）                             ┉┉6分

（2）的最小值是－1＋k              ┉┉┉8分

∴k=0                                                         ┅┅┅9分

此时

所以此时x的取值集合为                   ┉┉12分

练习册系列答案
相关题目
由函数y=f（x）确定数列{an}，an=f（n），函数y=f（x）的反函数y=f-1（x）能确定数列bn，bn=f-1（n）若对于任意n∈N*都有bn=an，则称数列{bn}是数列{an}的“自反函数列”
（1）设函数f（x）=
px+1
x+1
，若由函数f（x）确定的数列{an}的自反数列为{bn}，求an；
（2）已知正整数列{cn}的前项和sn=
1
2
（cn+
n
cn
）．写出Sn表达式，并证明你的结论；
（3）在（1）和（2）的条件下，d1=2，当n≥2时，设dn=
-1
anSn2
，Dn是数列{dn}的前n项和，且Dn＞loga（1-2a）恒成立，求a的取值范围．
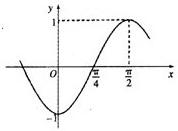精英家教网已知函f（x）=sin（ωx+φ）（ω＞0，|φ|＜π）的部分图象如图所示：
（1）求ω，φ的值；
（2）设g（x）=2
2
f（
x
2
）f（
x
2
-
π
8
）-1，当x∈[0，
π
2
]时，求函数g（x）的值域．
设x1，x2（x1≠x2）是函数f（x）=ax3+bx2-a2x（a＞0）的两个极值点．
（1）若x1=-1，x2=2，求函f（x）的解析式；
（2）若|x1|+|x2|=2
2
，求b的最大值．
（2009•金山区一模）已知等差数列{an}满足：a1+a2n-1=2n，（n∈N*），设Sn是数列{
1an
}的前n项和，记f（n）=S2n-Sn，
（1）求an；（n∈N*）
（2）比较f（n+1）与f（n）的大小；（n∈N*）
（3）如果函数g（x）=log2x-12f（n）（其中x∈[a，b]）对于一切大于1的自然数n，其函数值都小于零，那么a、b应满足什么条件？

已知函数．

（1）求的最小值；

（2）当函数自变量的取值区间与对应函数值的取值区间相同时，这样的区间称为函数的保值区间.设，试问函数在上是否存在保值区间？若存在，请求出一个保值区间；若不存在，请说明理由.

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网